Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Box Size
The end goal of this project is to make a mock galaxy catalogue for a WFIRST ultra deep field (UDF). In this post I will determine what simulation box size I will need in order to create a light cone (I plan to follow the notes by Hollowed 2019 ) the corresponding mass resolution. If we are not able to get the required resolution we will need to tile the simulations to create the light cone.
Ultra Deep Field
One advantage to UDFs with WFIRST is that it will cover 100x the area of Hubble and JWST surveys. The current status on the UDFs can be found in Koekemoer et al. 2019 . Overall, the UDF will have an area of \(\sim 1\,{\rm deg}^2\) and will probe to magnitudes of \(m_{AB}\sim 30\) at redshifts beyond \(z \sim 9-10\).
Box Calculation
First, I calculated the proper distance as:
\[\chi = \int_0^z \dfrac{c}{H(z')} dz'\]using the Friedmann equation to calculate \(H(z)\), with a Planck cosmology. Then, the angular diameter distance is:
\(d_A = \dfrac{S_k(\chi)}{1+z} = \dfrac{\chi}{1+z}\),
where in the last equality I assumed a flat cosmology.
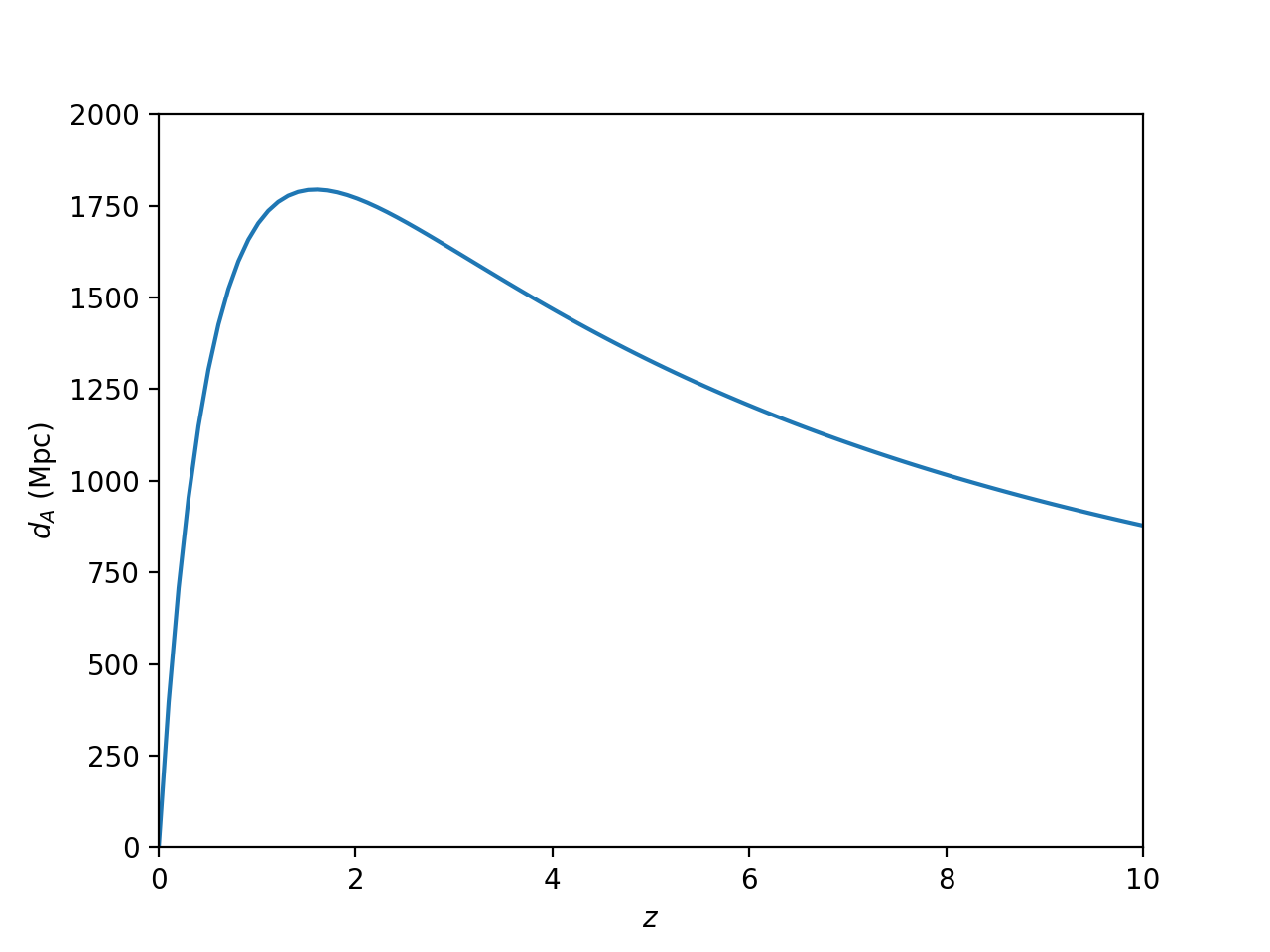
Then, if we consider that the actual size at redshift \(z\) is \(x=d_A \theta\), we can find comoving boxsize \(x/a = (1+z) x\) as a function of redshift for an angle of \(\theta = 1\, {\rm deg} = 0.017 \, {\rm rad}\), as shown in the plot below (remembering to multiply by \(h\)):
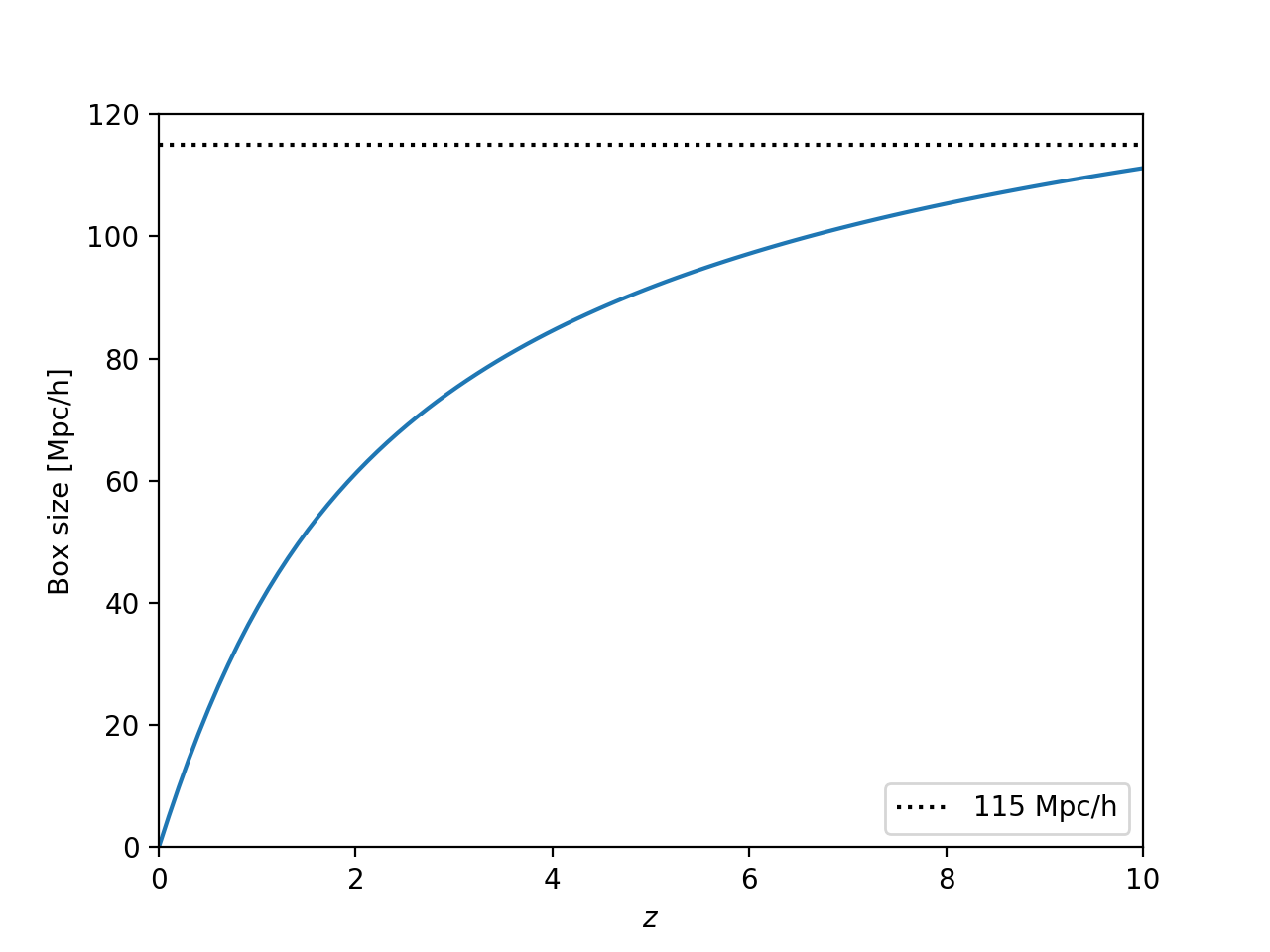
Bruno had calculated this in the past here and decided on a box size of \(115 {\rm Mpc} \, h^{-1}\). I don’t entirely follow his calculation, and he used \(\theta=0.78 \, {\rm deg}\) for the angle (I’m not sure where this number is from, but it might be more accurate than the one I am using). However, I also find that a boxsize of \(115 {\rm Mpc} h^{-1}\) seems reasonable.
Mass Resolution
To calculate the mass resolution in a box of \(115 {\rm Mpc}\, h^{-1}\), I first calculated the total mass in the box \(M = \rho_b \, {\rm boxsize}^3 = 3 H^2\Omega_M / 8 \pi G {\rm boxsize}^3\), and then divided it by the number of particles.
I found a total mass of \(8.69 \times 10^{16} M_{\rm sun}/h\), with resolutions of:
| Number of particles | \(128^3\) | \(256^3\) | \(512^3\) | \(1024^3\) | \(2048^3\) |
| Mass per particle \([M_{\rm sun}/h]\): | \(4.14 \times 10^{10}\) | \(5.18 \times 10^9\) | \(6.47 \times 10^8\) | \(8.10 \times 10^7\) | \(1.01 \times 10^7\) |
Bruno found similar (but not identical numbers) here .
Update: Bruno’s numbers are right, I had accidentally typed 2/8 not 3/8 in the above calculation.
Conclusions
Therefore, if we run simulations with a box size of \(115 {\rm Mpc}\, h^{-1}\) and \(2048^3\) particles, particles will have a mass of \(\sim 10^7 M_{\rm sun}/h\). Assuming that we will resolve halos with more than 100 particles, this means the smallest resolved halos will have masses of \(\sim 10^9 M_{\rm sun}/h\). This seems okay to me (but I will see what Brant thinks). The other option is to use a smaller box size and then tile them.