Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Check Image Noise
In this post I am double checking the noise is added properly to the synthetic images. I will be using the H158 filter for test image, with an exposure of 40 hours.
First Glance
First, I am going to compare by eye our H158 image with the XDF, in filter f435w, downloaded from https://archive.stsci.edu/prepds/xdf/. These images should have similar depths. Putting both in ds9, and scaling with the “zscale” option, they look as follows (ours is on the right, the XDF is on the right; note these are NOT scaled the same, and are NOT covering the same area).

At first glance, it looks like the noise levels in our image are much too low. But I need to check this quantitatively, in case it has to do with the way the images are displayed.
The typical fluctuations in the background pixels in our image are about 0.035 nJy (see the image below for how I estimated this), while in the XDF image about 0.00045 electrons/s/pixel.
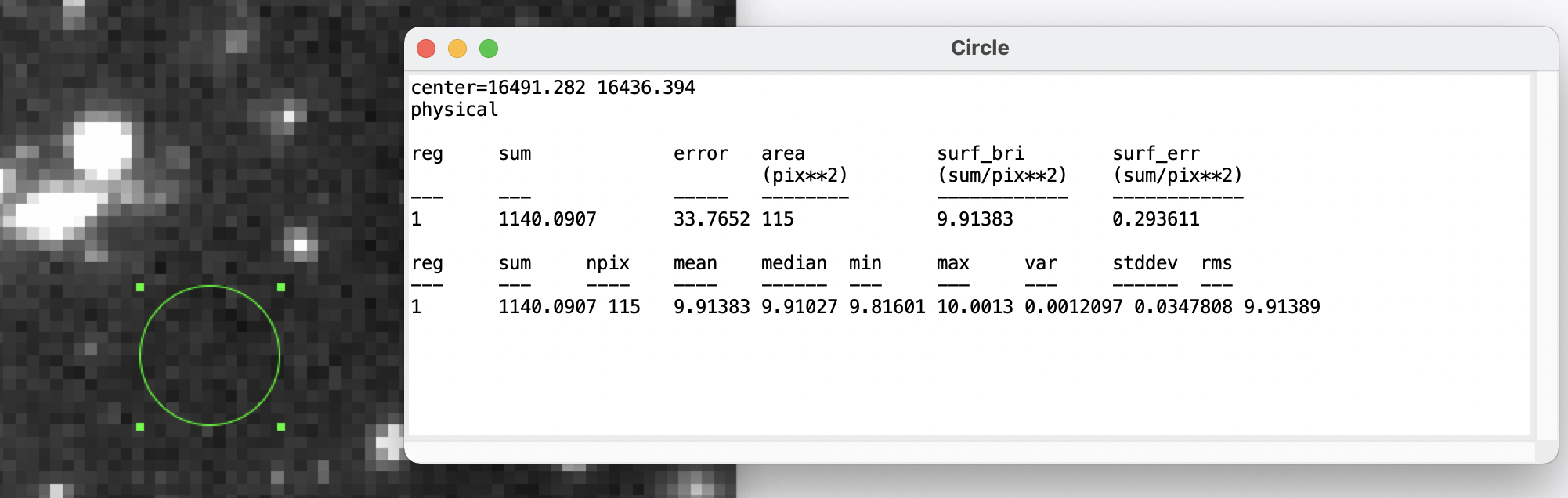
To convert the value of 0.035 nJy to photon counts for a comparison, I first divided by Plancks constant, to get 5.28e-08 counts/s/cm^2. For a collecting area of 37570 cm^2, this is 0.0019 counts/s/pixel (we are assuming one photon corresponds to one electron). Our image has pixels that are 0.11 arcseconds across, while the XDF image is 0.03 arcseconds. Accounting for the difference in pixel size, our image has roughly 0.0001 electrons/s/pixel. This is about a factor of 5 lower than the XDF, which sounds okay, given that it is a rough comparison!
So from first glance, the noise does seem reasonable! In this post I will do a few more sanity checks.
The SNR of the image
If I consider an aperture, the fluctuations in the aperture should be \(\sqrt{N} \sigma\), where \(\sigma\) is the standard deviation in the background pixels, and \(N\) is the number of pixels.
For an aperture of 0.2 arcsec^2 (which I think is what they used in GOODS and CANDELS), this corresponds to \(N=16.5\).
For a background fluctuation of 0.035 nJy, as estimated above, this gives a \(5 \sigma\) detection of 0.7 nJy = 31.8 mag.
This is higher than the expected magnitude of 30. This corresponds to the noise being a factor of 5 lower than expected, which is consistent with what I found above.
How The Noise Is Added
1) Start with galaxy image
2) The sky background is added
3) Poisson noise is added to the galaxy and sky background image
4) Other sources of noise, including detector noise, read noise, dark current, ect., are added.
5) The image is converted to nJy
1) Are the original fluxes of the galaxies assigned correctly?
Bruno checked that the flux of an individual galaxy sums to the assigned flux, so I am fairly confident that the fluxes are being assigned appropriately! Another possible issue is that the assigned flux i gave him is not in the correct units.
In the catalog, the galaxies each have an apparent magnitude, mag. Galsim requires the flux in units photons/cm^2/s. I did the conversion as follows:
planck = 6.626196e-27 #erg s
f_nu = 10**((mag+48.6)/(-2.5)) #erg s−1 cm−2 Hz−1
f_nu = f_nu/planck # counts/s/cm^2
There is a description of here of the way galsim handles units. Given the exposure time, collecting area and gain, the image should be in ADUs.
2) Does the sky background look reasonable?
The image sky background is from sky level + thermal background. Thermal background could be a significant noise contribution for Roman, and comes from several sources, including the telescope, optics of filters, ect.
Looking at this exposure time calculator manual for Roman, there are some example outputs of sky and thermal background flux values. It seems like on the order of 1 e-/pix/s is reasonable for the sky background and 0.1 e-/pix/s is reasonable for the thermal background. I will use these numbers for a sanity check.
For ours, the sky level and thermal background are approximately 6200000 e-/arcsec^2 and 3000 e-/pixel, respectively. Dividing that by the exposure time, and taking into account the pixel size I get 2 e-/pixel/s and 0.008 e-/pixel/s.
Overall, this is reassuring that the noise level is the right order of magnitude, though these aren’t really direct comparisons (e.g. for the example values, I don’t know where they are pointed on the sky, or which filters they are using).
3) Is the Poisson noise added correctly?
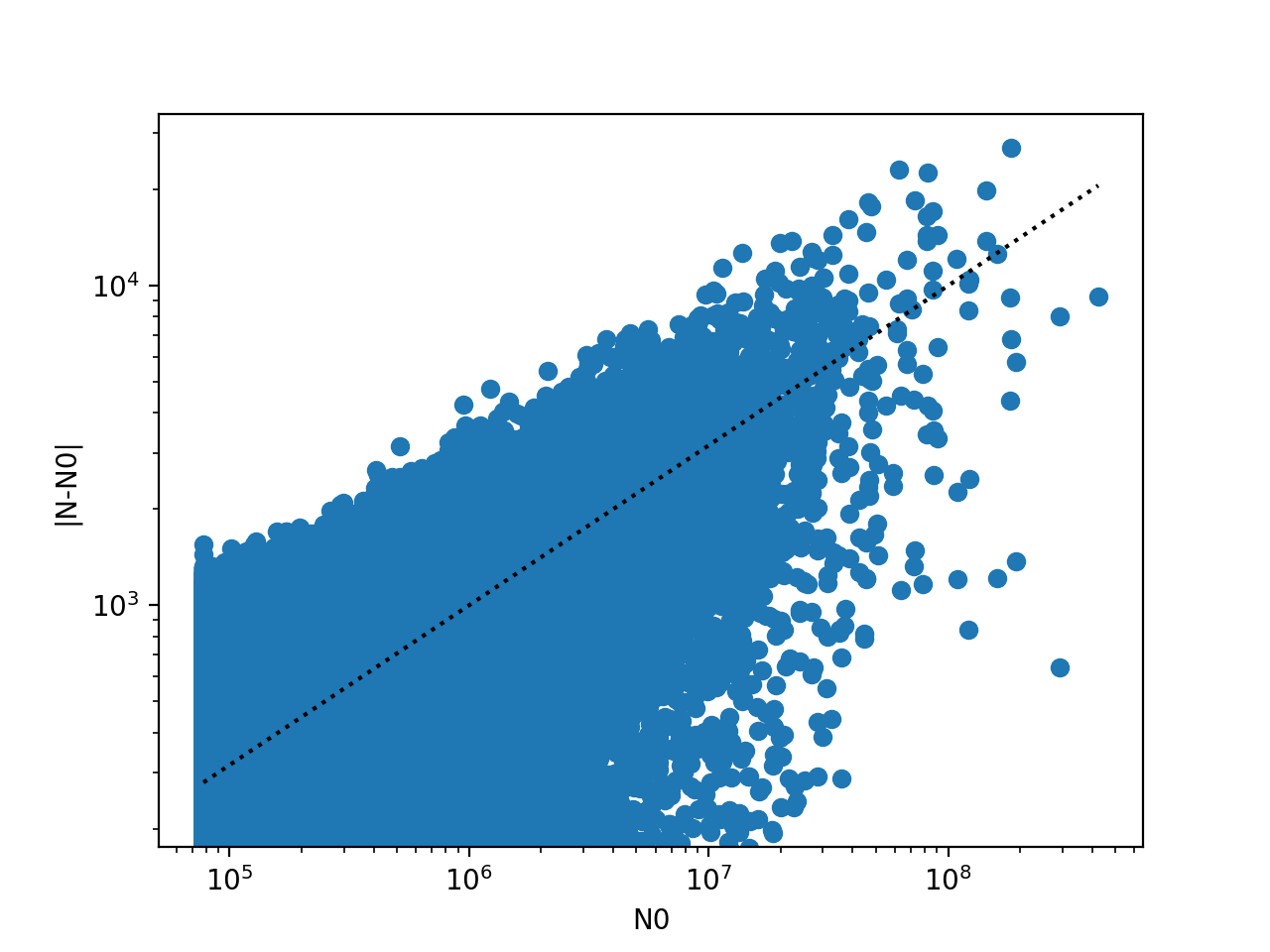
I checked the poisson noise by taking the number of counts, N0 in each pixel before adding the noise, and then looking at the signal after, N.
The scatter plot below shows the noise added in a pixel as a function of N0. The dotted line is the square root of N, which should be the average noise added for Poisson error. This looks good.
4) Additional sources of noise added correctly?
I expect that this source of noise is subdominant, and so did not look into it in this post. It seems unlikely that this would account for a factor of 5 in the noise level.
5) Image converted to nJy
The image is converted back into nJy using the same conversion as above. i.e.
h_planck = 6.626196e-27 #ergs sec
nJy_conv = 1e32 # 1/[erg/s/cm^2/Hz]
conversion = nJy_conv * h_planck / collecting_area / exposure_time
Next steps
1) Try and figure out where the factor of 5 is coming from
Double check how galsim treats the zeropoints of the filters, and that we have defined those correctly.
Do a more careful calculation of the SNR, by subtracting off the (known) background, and calculating the rms in the background. Comparing this in all the filters to see if they all seem off by a factor of 5.
2) Look into different image artefacts
There are a few image artefacts that may or may not be problems. We should at least understand them as best as possible! The first is that the PSF spikes look very strong. This could be a feature of Roman, or just due to the nonlinear scaling of the images. The second issue is that some of the bright galaxies have rings around them, that look like diffraction patterns.
Things to fix when regenerating images
1) Use the WCS described in this post for creating the image and sky background.
2) Make sure to save the header with the FITS files, including the WCS information.