Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Galaxy Sizes Part I
This post is on assigning galaxy sizes to each mock galaxy. The galaxy sizes will be characterized in terms of the half-light semimajor radius, \(R_{\rm eff, maj}\). For now I am following Williams et al. 2018.
Below Redshift 4
The parametrization for \(R_{\rm eff, maj}\) is from van der Wel et al. 2014, and is given by:
\[R_{\rm eff, maj} = B_H(M_\odot) \left( \dfrac{H(z)}{H_0}\right)^{\beta(M_\odot)}\]The coefficents \(B_H(M_\odot)\) and \(\beta(M_\odot)\) for star-forming and quiescent galaxies are given in Equations 24 and 25, respectively.
Here is the plot from Williams et al (their Fig 15):
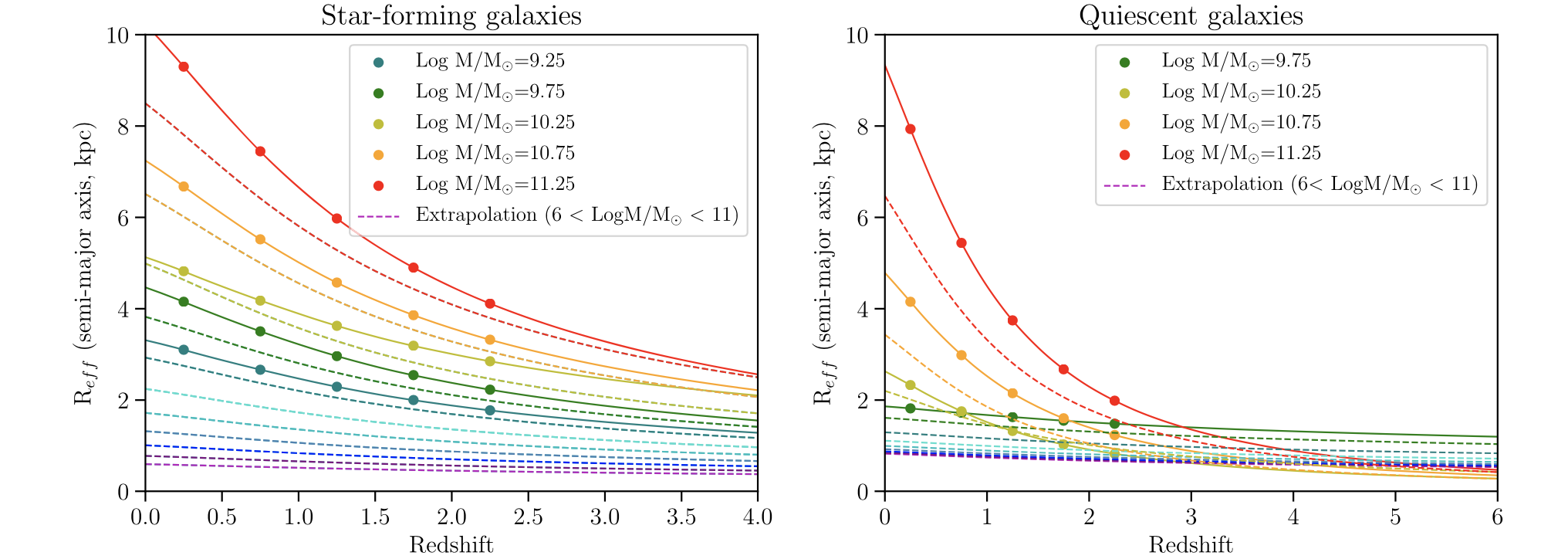
There must be a mistake in their parameterization, as I can’t reproduce their plots. My best guess is that the fit for \(B_H\) is actually in \(\log_{10}B_H\). With this I can almost reproduce their Fig 15, but it still looks a little off:
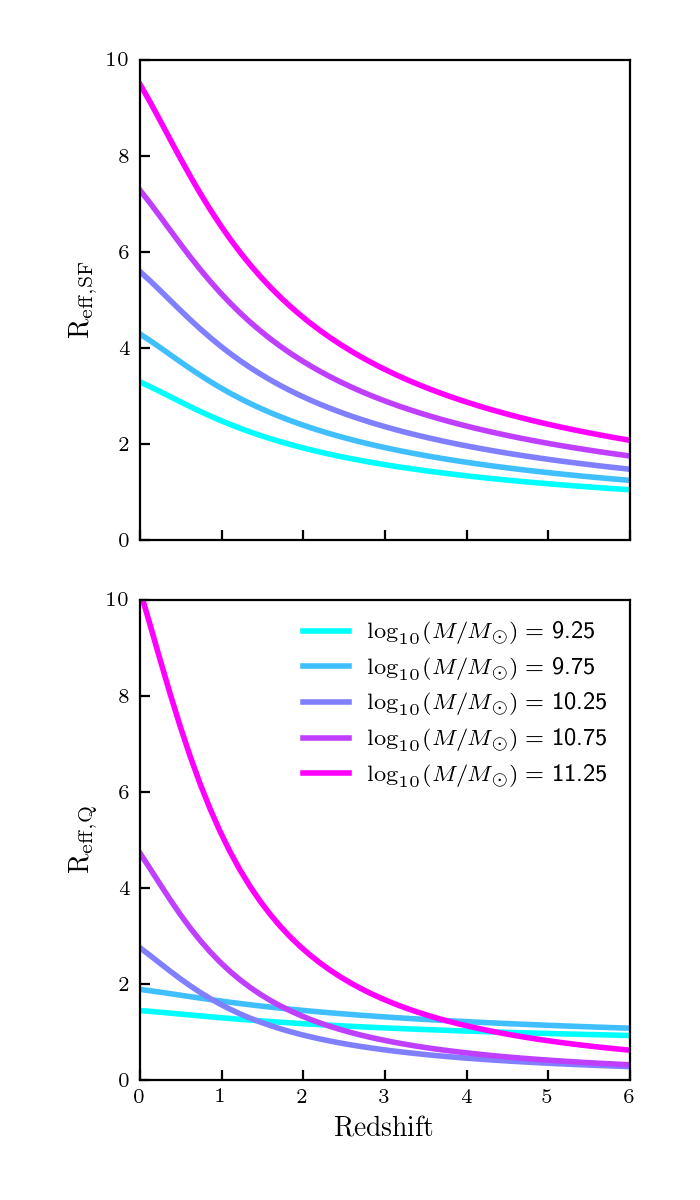
Above Redshift 4
Since there are no constraints at higher redshifts for quiescent galaxies, this relationship will be extrapolated to these redshift ranges.
For starforming galaxies, above redshift 4, they are constrained by luminosity functions. The constraints are in terms of the circularized half-light radius
\[R_{\rm eff, circ} = R_{\rm eff, maj} \sqrt{b/a}\]This requires setting the galaxy shape, which I’ll address in a later post. \(R_{\rm eff, circ}\) can be calculated from the relation
\(R_{\rm eff, circ} = 6.9 (1+z)^{-1.2} \left(\dfrac{L_{\rm UV}}{L_0} \right)^{0.27}\),
where \(L_{\rm UV}\) is the UV luminosity, and \(L_0\) is a characteristic luminosity corresponding to a magnitude of \(M_{\rm UV}=-21\).
We have the UV magnitudes (though I am not sure that the UV band is defined the same in this equation; I should double check I don’t have to correct for this). Then, magnitudes are related to luminosities according to:
\[M_2 - M_1 = 2.5 \log_{10}(L_1/L_2)\]Therefore,
\(R_{\rm eff, circ} = 6.9 (1+z)^{-1.2} 10^{0.27(M_{\rm UV} +21)/2.5}\).
To-Do
1) Find out why I am not reproducing Fig 15 from Williams et al.
2) Double check that I am using the right UV magnitude in the equation for star-forming galaxies above redshift 4.
3) Assign sizes to galaxies, with appropriate scatter (\(R_{\rm eff, maj}\) for low redshift galaxies, and \(R_{\rm eff, circ}\) for high redshift galaxies).
4) Assign galaxy shapes and use these to calculate \(R_{\rm eff, maj}\) for the high redshift galaxies.
5) Check the distribution/scatter of galaxy sizes in our mock catalog look right .
6) Check that trends in galaxy size–halo size seem reasonable.