Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Light Cone Tests
In this post I outlined the plan for making a light cone. In the current post, I’ll summarize what I currently have working, and test it on a sample simulation.
Tiling Simulations
Because the survey is deep but doesn’t cover a lot of area, the plan is to tile simulation boxes in one direction; the length of the box should be large enough to cover the area of the sky at high redshift (as calculated here). Therefore, the code will loop through each tiled box, until it reaches the needed depth of the simulation (I found Bernyk et al. 2016 to be a helpful reference for how to do this).
Here is a plot of comoving distance versus redshift, and the corresponding number of 115 Mpc/h boxes:
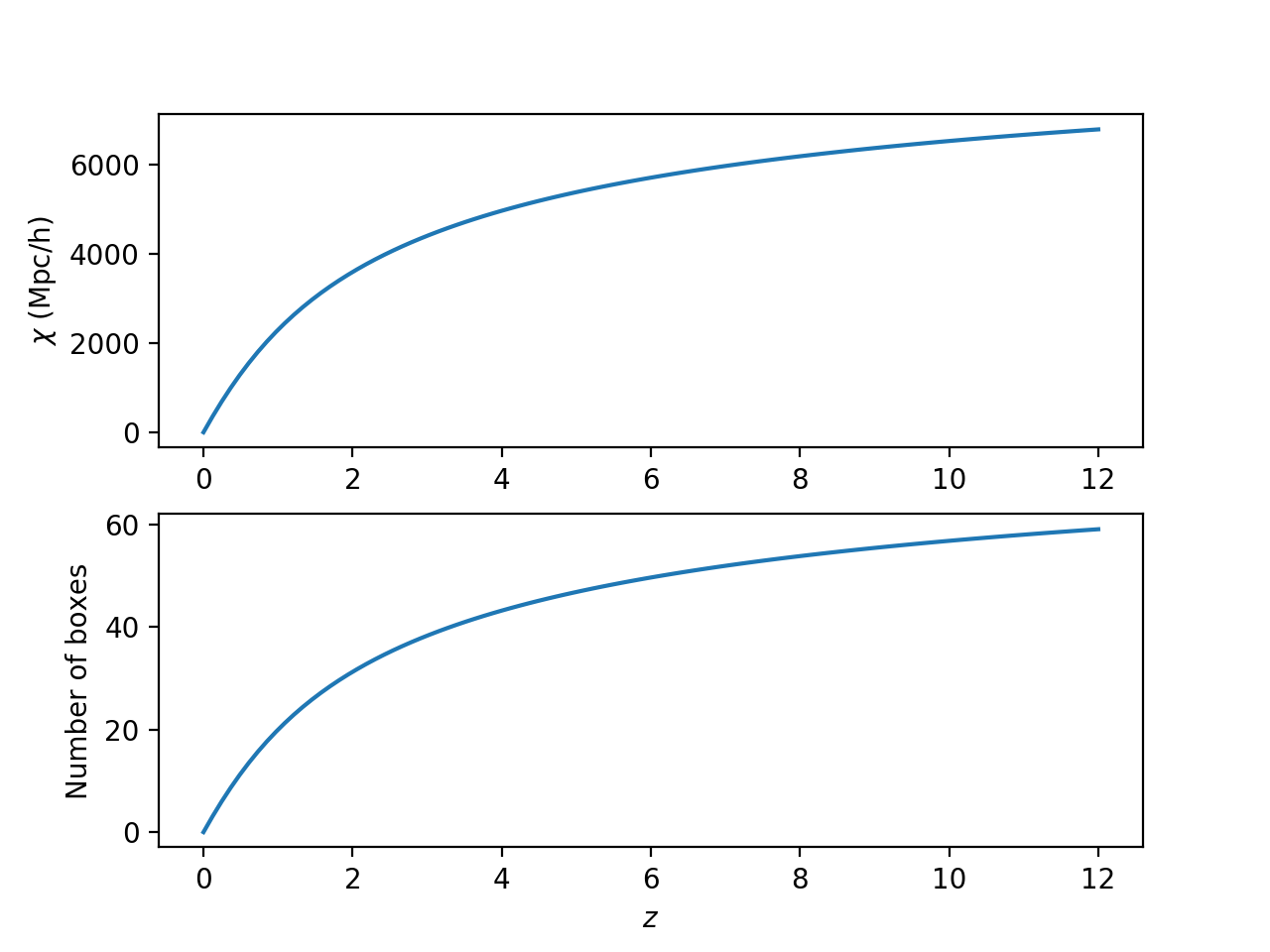
This means we will need to tile 57 boxes to go out to redshift 10, and 60 to go out to redshift 12. For now, I am just tiling 20 boxes, which corresponds to a redshift of 1.
Outline of Code
1) From the AHF tree output files, find out which halo IDs map to the progenitors in each snapshot (I generate an array to store this information).
2) For each tiled box, randomly translate, reflect and permutate the box axes; also calculate the offset needed for the box (the velocities of each halo are also reflected/permutated appropriately).
3) For the given box, start with the most recent snapshot, and load all the isolated halos (ignore subhalos; these will be kept with their hosts).
4) For each halo, find its progenitor and get both of their positions
5) Calculate the time the halo would cross the light cone, \(t_e\) , from these positions (Equations 27-29 in Korytov et al. 2019). If this time is inbetween the snapshot times \(t_{j+1}\) and \(t_j\), it crossed!
6) If the halo crossed, use \(t_e\) to get the redshift of the halo, and interpolate for the position and velocity of the halo—technically I am using the velocity \(v_{\rm lin}= (r_{j+1}-r_j)/(t_{j+1}-t_j)\) and calculating the position as \(r = r_j + v_{\rm lin}(t_e-t_j)\). I then save all other halo properties (mass, substructure, ect.) from the halo at snapshot \(j+1\).
Potential Problems
1) Right now it is possible to count the same halo more than once, if it crosses the light cone at multiple times; this could be easily checked and these halos could be removed. I just need to code this.
2) As in Korytov et al. 2019, I am assigning the mass of the halo based on its mass in snapshot \(j+1\). Another approach is to allow the merger of halos to happen at a time randomly between the two snapshots; the properties would then depend on whether \(t_e\) is before or after this time (this is the approach in Smith et al. 2017). A more physical approach, as suggested by Brant, is to look at the dynamical times of the halos to decide when the merger happened. I like this idea, and later I will think about how to calculate this, and try and implement it.
3) Deciding on the progenitor of the halo does have some ambiguity: I am using AHF, which assigns a progenitor based on a merit function that considers the number of shared particles. This is different than Korytov et al. 2019 who use the most massive progenitor. I don’t think this will be a problem.
4) If a halo is created between snapshot \(j\) and \(j+1\), I don’t consider whether it could have crossed the lightcone in that time. This probably won’t happen often with the high number of snapshots I am using. However, I want to eventually account for these cases by interpolating for the position of the halo in snapshot \(j\) using it’s velocity.
5) Since I am rotating and stacking boxes, there will be discontinuities at the borders of the boxes. As I am taking halo positions, rather than individual particles, I shouldn’t truncate any halos or filaments—however, there will still be artifacts. From the literature, it appears that these won’t be very important (as long as I consider scales smaller than the box). However, I can try to fix this a bit by (a) stacking some boxes without rotation, and choosing the survey volume through the box so it doesn’t intersect the same parts of the volume more than once and/or (b) choosing translations/rotations to try and preserve the mean densities at the borders.
6) Another issue is that my code is slow right now, and may take too long to run on the 2048 simulations. I can optimize a few things; e.g. I can pre-calculate what range of redshifts are possible for each tiled box, and only loop through those snapshots. Also, right now I am storing the merger histories for all the halos in one numpy array (step 1)—this isn’t feasible with the larger halo catalogs. It might be trivial to parallelize my code as well; for example, each tiled box can run independently.
Some Sample Results
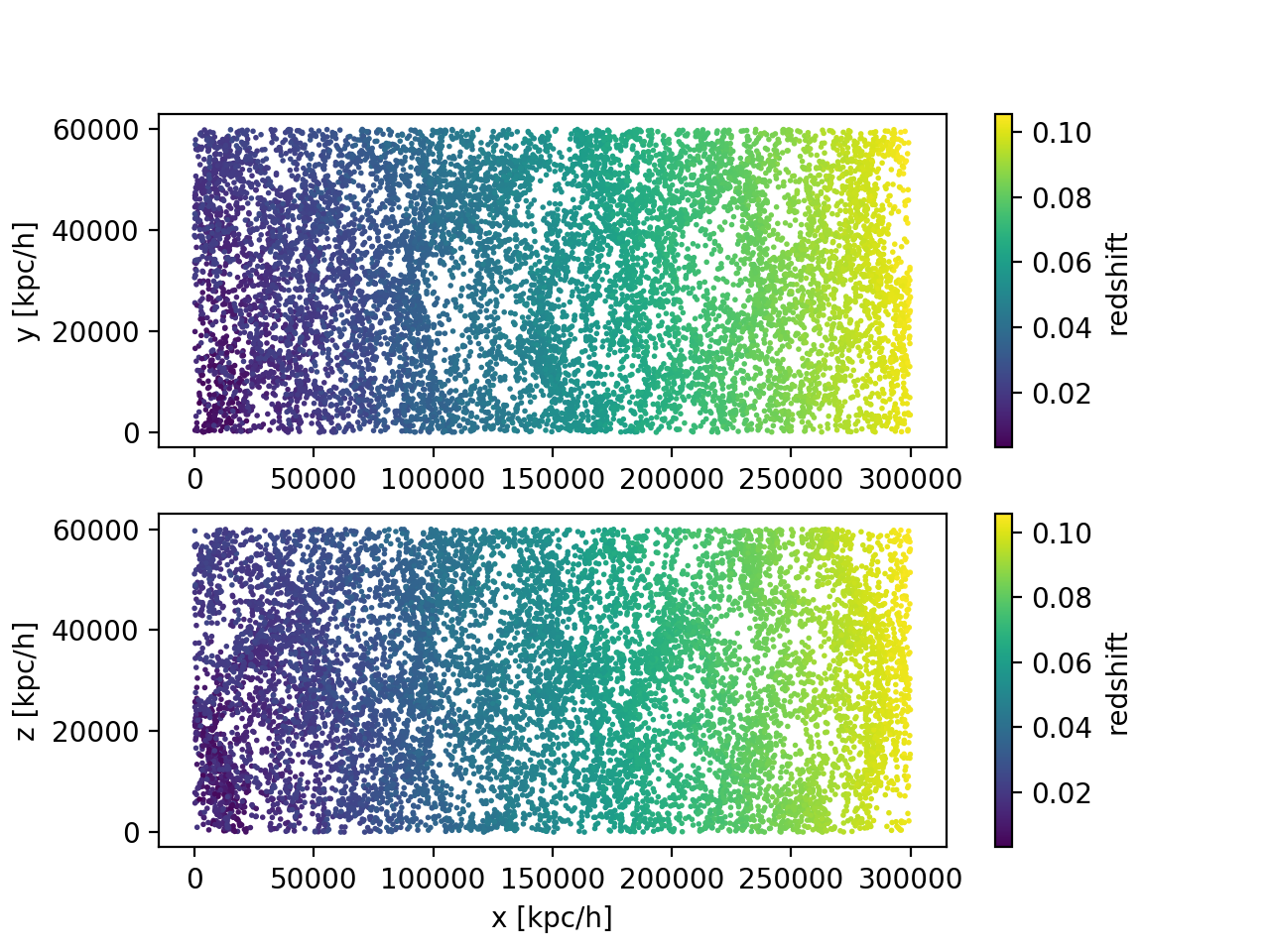
I wanted to test this on the 512 simulations, but the code is still running to generate the lightcone catalog. So, I am going to test a couple things on the sample \(256^3\) test simulation I have; it has a box size of 60 Mpc, and a WMAP-ish cosmology? (I can’t figure out exactly what cosmology it is). I have tiled 5 boxes, which has a depth corresponding to a redshift of roughly 0.1.
Here is the position of these (isolated) halos in real space, colored by their assigned redshifts:
Next, I am checking that the halo mass functions look reasonable, by comparing my lightcone output to the final snapshot:
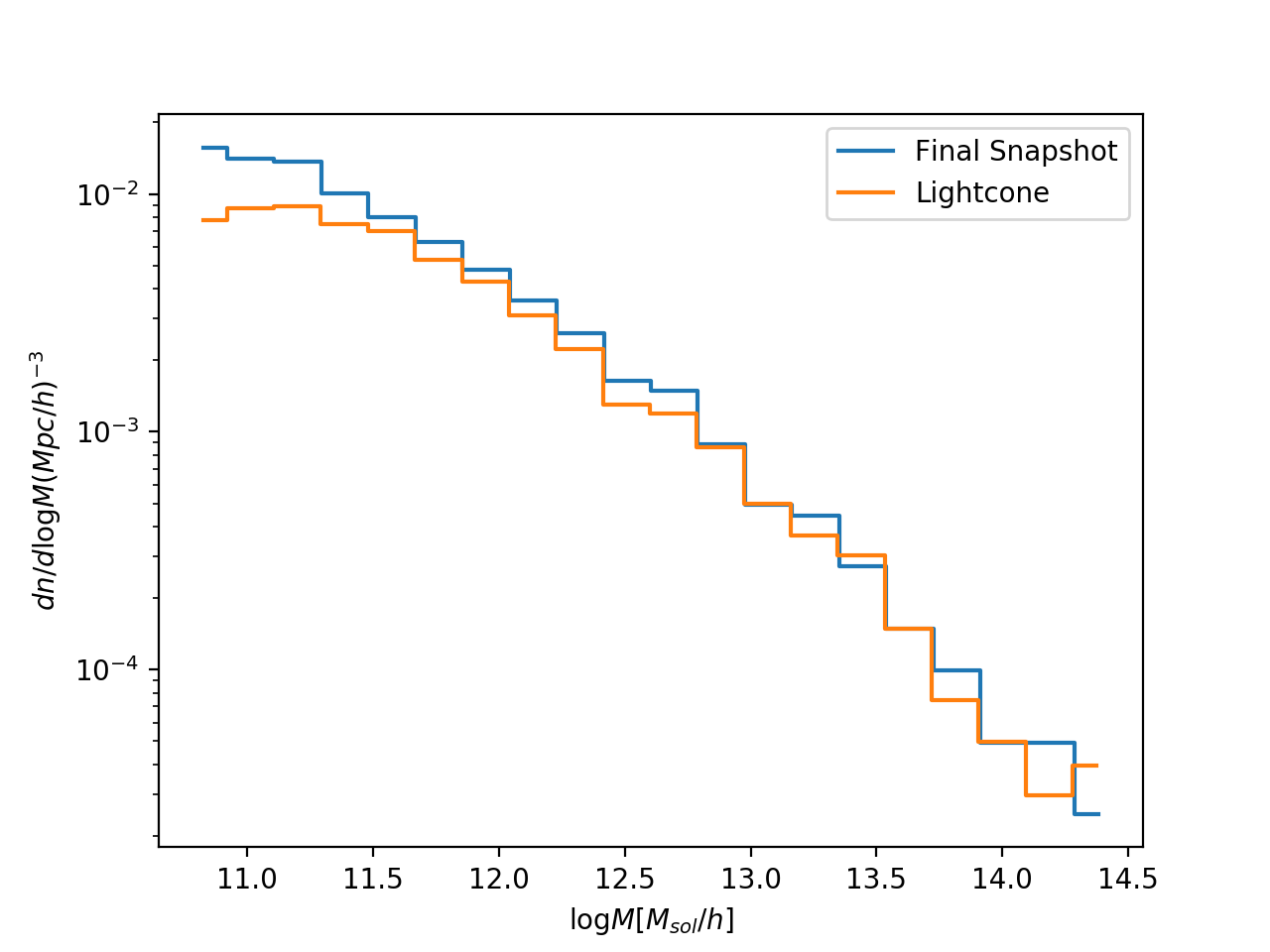
So far this looks pretty good. There is a bit of difference at the low mass end… I’m not sure why this is. One possibility is that it is from potential problem (4).
Next Steps
1) Run this for the 512 Simulations. Right now my code isn’t very efficient, and is taking a long time to run. I might try and optimize this a bit over the next few days.
2) Determine which halos are in the survey volume. For now, I am not doing any fancy geometry, so this should be easy.
3) Abundance matching. I have previously written code to do this at redshift zero. I need to double check that this works (there were a couple of potential issues in the scatter model), and extend it to larger redshifts. I will also need to write a little bit of code to read in the IDs of subhalos associated with each isolated halo
4) Go through some of the potential problems in my light cone method, as outlined above.