Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
SED Methods Part II
This is an up-to-date summary of the method I’m using to generate SEDs. The last summary was in this post, and also there were some updates (e.g. here).
Method
To begin, each galaxy has a redshift \(z\) (from the lightcone generation), a mass, \(M\) (from abundance matching), and morphological properties (from scaling relations). Additionally, each galaxy is either labelled as star-forming (SF) or quiescent (Q), as sampled from the SMF.
Given the cosmology, we can also calculate \(t_{\rm age}\) which is the cosmological time at redshift \(z\).
Age
First, we choose the age of the galaxy, \(a\). Note that my method of assigning ages is probably the least well-motivated method out of all the parameters.
The age, \(a\) was sampled from a truncated gaussian in \(\log_{\rm 10}(a/{\rm yr})\) with a standard deviation of 0.7 (motivated by W18).
The gaussian was truncated between 6 and \(\log_{10}(t_{\rm age}/{\rm yr}-10^6)\) for both SF and Q galaxies
For SF galaxies, as in W18, the Gaussian was centered at \(\log_{\rm 10}(a/{\rm yr})=9.3\). Since Quiescent galaxies should be older, I centered the ages for this on 9.8; this corresponds to a difference of 4 Gyr, and was motivated by this paper.
In this implementation, there is no dependance of age on mass, and no direct dependence on redshift (though since the gaussian is truncated based on the age of the universe, lower redshift galaxies will be on average older).
Then FSPS parameter sf_start is then \(t_{\rm age}-a\)
SFR
The SFR, \(\psi\) is described using a delayed tau model, in which
\[\psi(t) \propto t \exp{-t/\tau}\]FSPS normalizes this, such that the total mass created over the star formation history is \(1\, M_{\odot}\). This means that the current star formation rate of the galaxy is:
\[\psi_{\rm N} = \dfrac{a}{\tau^2 -(\tau^2+ a \tau)\exp^{-a/\tau} } \exp{-a/\tau}\]To scale this to the galaxy, we need to know (1) \(M\) and (2) the fraction of the mass we expect to survive at time \(t_{\rm age}\).
To calculate \(\psi\), I am following Shreiber et al. 2017 (equations 10 and 12 for star-forming (SF) and quiescent (Q) galaxies, respectively).
\(\psi\) not explicitly set in FSPS, but it is related to the age, e-folding time and mass of the galaxy
As a consistency check, I also evolved the SFR–mass relation backwards to see if the relation still held here, and it does seem reasonable.
Metallicity
As in W18, we set the stellar and ISM metallicity to be equal, \(Z\)
We get \(Z\) for SF galaxies from the fundamental metallicity relation (eq 15 in W18). I am also following their scatter model (eqs 16-17). I am using a truncated distribution though, with \(-2.2<Z<0.24\).
For Q galaxies, \(Z\) is sampled uniformly from the range \(-2.2<Z<0.24\).
Here is a closer look at the metallicities; overall, this assignment seems reasonable (I also check some of the SFR properties in this post).
The FSPS parameters are logzsol and gas_logz.
Gas Ionization
\(U_S\) is selected from \(Z\)–\(U_S\) relation (eq 18 in W18), with a scatter of 0.3 dex sampled from a student’s t-distribution. I am truncating the distribution such that \(-4<\log_{10}{U_S}<-1\).
This should really only be for SF galaxies; this parameter shouldn’t matter for Q galaxies, so for now I am calculating \(U_S\) for Q galaxies the same way. I need to check that that is reasonable.
The FSPS parameter is gas_logu.
Dust Attenuation
I have updated this to include the galaxy shapes (see previous implementation here).
The dust attenuation can be calculated from the \(\psi\)–\(Z\)–\(\hat{\tau}_{V}\). To do this, Williams et al. follows Devriendt et al 1999.
First, you can calculate the \(V\) band, face-on attenuation optical depth:
\[\hat{\tau}_{V} =\left(\frac{Z_{\mathrm{ISM}}}{Z_{\odot}}\right)^{1.6}\left(\frac{N_{\mathrm{H}}}{2.1 \times 10^{21} \mathrm{cm}^{-2}}\right)\]The mean hydrogen column density can be determined from the cold gas fraction:
\[N_H = 6.8 \times 10^{21} \dfrac{M_{\rm gas}}{M_* + M_{\rm gas}}\]To calculate \(M_{\rm gas}\) you can use \(M_{\rm gas}=\Sigma_{\rm gas} \pi r^2\), and then relate \(\Sigma_{\rm gas}\) to \(\Sigma_{\rm \psi} = \psi/(\pi r^2)\) using the Kennicutt-Shmidt relation:
\[\dfrac{\Sigma_{SFR}}{M_\odot {\rm yr}^{-1} {\rm kpc}^{-2}} = 2.5e-4 \left(\dfrac{\Sigma_{gas}}{M_\odot {\rm pc}^{-2}}\right)^{1.4}\]You can then convert this face-on attenuation to the average galaxy dust attenuation averaged over inclination angles (equation 21 in Williams). For now I am just using this averaged attenuation parameter.
As in W18, I neglect dust for quiescent galaxies (i.e. set dust2 to zero). I am not sure how justified this is.
The FSPS parameter is dust2 (with the dust model we are using, dust1 must be set to zero).
Star-formation Time
Finally, we get the e-folding time, \(\tau\). Since this is dependent on the surviving stellar mass fraction, \(x\) (stellar_mass in FSPS) this has to be calculated last.
To get this, I iteratively solved for \(\tau\) from \(\psi(\tau) = \psi_N(\tau) \times\dfrac{M}{x}\), updating \(x\) on every iteration. In practice, it only takes a couple of iterations for \(\tau\) to converge.
I impose a maximum \(\tau\) of 100 Gyr. Larger values than this have little effect on the SFR. This means that there will be many galaxies with \(\tau=100\), but I think that is okay.
Summary of free parameters
The parameters for SFR, metallicity, gas ionization and star formation times all seem reasonable. I do want to look into age and dust attenuation more carefully.
Checking How Realistic the SEDs are
The two main things that I want to check make sense are (1) the UV properties and (2) the galaxy colours.
Here are these results with the updated SED catalog.
UV Properties
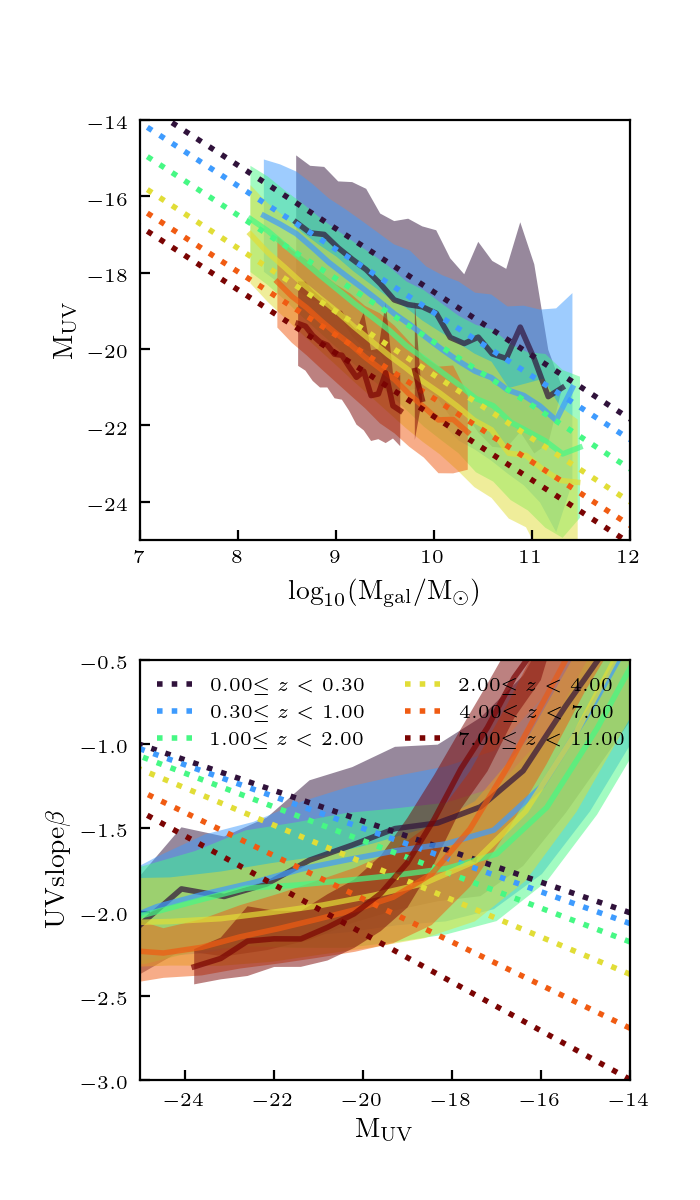
The turnover on the right end of the bottom plot might be partially because I am missing faint low mass galaxies (since this looks a bit better on the “analytic” catalog, in which I generated masses from the SMFs, without using the simulations). However, there is still clearly problems here.
Colour Properties
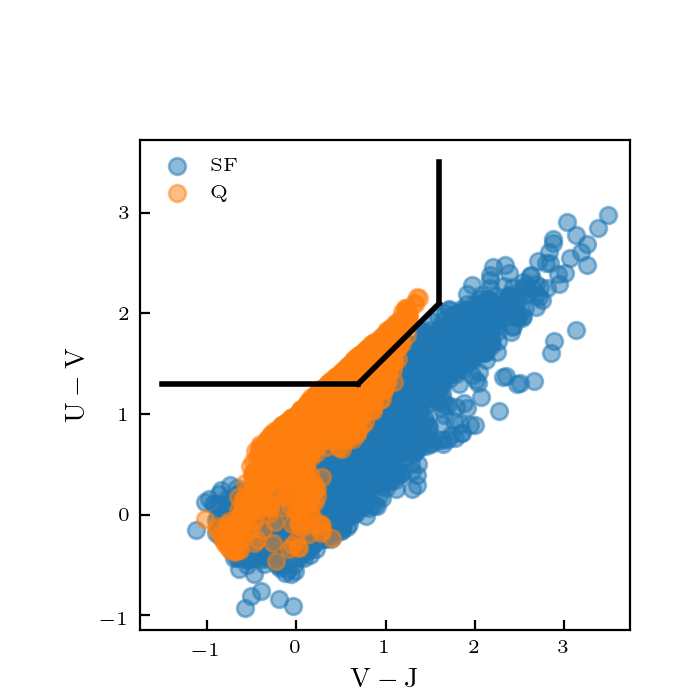
This again doesn’t look right again… As shown earlier, this is sensitive to the age assignments, so my Quiescent galaxies are probably too young.
Things to check
1) Are there any constraints of galaxy ages in the literature that I can use to check if my ages are reasonable?
2) How much do different ages affect the UV properties? (Plan: generate 1000 mock galaxies at redshift 0 with the same mass; see the relation between age and UV properties).
3) Does the gas ionization parameter matter at all for Quiescent galaxies? Is it okay how I am setting it now?
4) Do my dust attenuation values make sense? How can I check this?
5) Are my beta values calculated correctly? Check spectra.