Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
SEDs from Mean Relations
We had decided to use FSPS to create SEDs, as outlined here. We also identified five potential free parameters, and how they affect the UV properties we are trying to match here
In this post, I will outline a quick way of assigning SEDs based on mean relations. We will likely improve this later, to account for scatter in the relations.
Gas Ionization Parameter
The gas ionization parameter, \(U_S\) (gas_logu), does not seem to affect the UV properties much. We can use the relation from Carton et al. 2017 to relate the metallicity, \(Z\) and \(U_S\). (This relation is for low redshift only, but we will neglect that for now).
Star Formation History
Before, we identified logzol,tau,sf_start,dust2 and gas_logu to be the parameters we wanted to control.
The parameters tau and sf_start control the SFH. It is probabliy more natural to talk in terms of the star formation history, \(\psi\) and the age of the galaxy, \(a=\)t_age - sf_start.
We have chosen to describe the SFR by a delayed tau model:
\[\psi(t) \propto t e^{-t/\tau}\]FSPS normalizes this so that one solar mass of stars is created over the age of the universe. The time, \(t\), ranges between sf_start and t_age and \(\tau\) is the star formation rate (tau).
The normalization constant can be calculated as \(C = M_{\rm gal}/\)stellar_mass, and \(\psi\) is then:
To describe the SFR, we will use the fundamental metallicity relation \(M_*\)–\(Z\)–\(\psi\) (Eq 15 in Williams, but see also Hunt et al. 2016):
\[\log{Z_{\rm ISM}/Z_\odot} + 8.7 \approx -0.14 \log(\psi/M_{\odot}{\rm yr}^{-1}) + 0.37 \log(M/M_{\rm odot})+4.82\]Therefore, you can express \(\psi\) in terms of the metallicity and galaxy mass.
Dust
The dust attenuation can be calculated from the \(\psi\)–\(Z\)–\(\hat{\tau}_{V}\). To do this, Williams et al. follows Devriendt et al 1999.
First, you can calculate the \(V\) band, face-on attenuation optical depth:
\[\hat{\tau}_{V} =\left(\frac{Z_{\mathrm{ISM}}}{Z_{\odot}}\right)^{1.6}\left(\frac{N_{\mathrm{H}}}{2.1 \times 10^{21} \mathrm{cm}^{-2}}\right)\]The mean hydrogen column density can be determined from the cold gas fraction:
\[N_H = 6.8 \times 10^{21} \dfrac{M_{\rm gas}}{M_* + M_{\rm gas}}\]To calculate \(M_{\rm gas}\) you can use \(M_{\rm gas}=\Sigma_{\rm gas} \pi r^2\), and then relate \(\Sigma_{\rm gas}\) to \(\Sigma_{\rm \psi} = \psi/(\pi r^2)\) using the Kennicutt-Shmidt relation. I haven’t assigned galaxy sizes yet, so for now I am just going to assume that \(M_{gas}=10^9 \psi\). My reasoning is that about 10% of the gas should be converted to stars every \(10^8\) years.
You can then convert this face-on attenuation to the average galaxy dust attenuation averaged over inclination angles (equation 21 in Williams). For now I am just using this averaged attenuation parameter.
The Final Two Parameters
Now we have two free parameters, metallicity and galaxy age that we want to use to fit \(M_{UV}\) and \(\beta\).
If we explore this in parameter space:
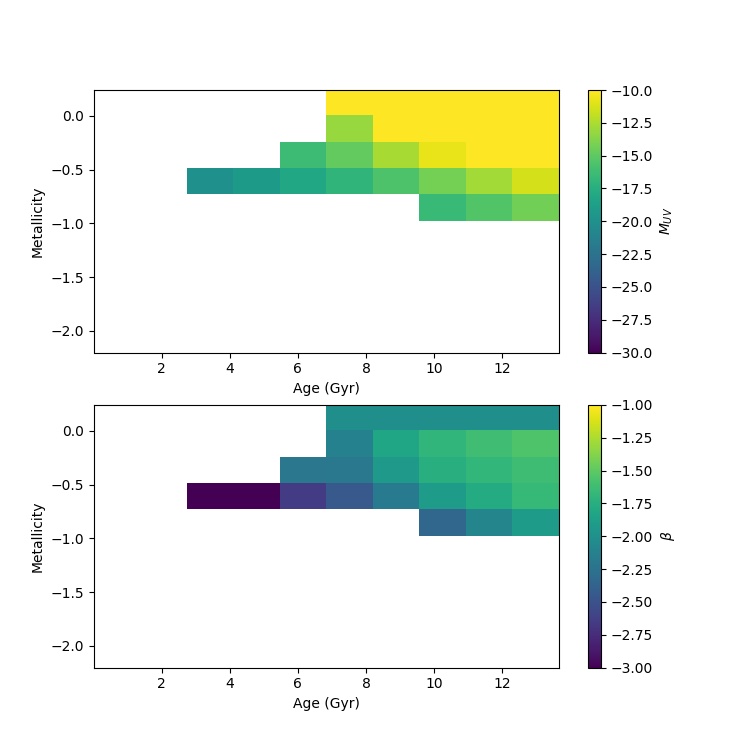
Note that the white regions are where the star formation time, \(\tau\) was too low to be feasible. Overall we have two parameters and two unknowns; this could be used to fit the metallicity and galaxy age using a local minima solver.
Next Steps
I now have a rough method for assigning SEDs.
1) The method outlined in this post is for star-forming galaxies. I will need to also assign to quiescent galaxies. The procedure from Williams et al. is given in Section 4.2. They chose age, star formation timescale and metallicities from uniform distributions. gas_logu does not need to ne assigned. In Williams et al. they also neglected dist attenuation—I will copy this for now, but I am not sure how reasonable this is.
2) How long does this take to assign SEDs to each galaxy? Will I need to speed it up? (Might be better to do a grid and interpolate along it…)
3) If I try and recover all these relations from the mock catalog, do they look reasonable? How is the scatter? Will this be accurate enough for our purposes?
4) Given the SEDs, I need to recover the magnitude in the different bands. For now, I’ll just use some built-in filters to get it working, but I should get the proper filter information from Brant.