Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Vpeak Function
This is a summary for where we are in the abundance matching procedure:
(1) Halo mass proxy: \(v_{\rm peak}\)
(2) Stellar mass function: I have a parameterized form from Li & White 2009, but we will need to update this to a more recent model that extends to higher redshifts, as in Williams et al. 2018
(3) Halo \(v_{\rm peak}\) function: before I had been measuring this from the simulation, but once adding scatter this becomes problematic outside of the range of the data. Also it becomes a problem below the resolution limit of the simulation. In this document I will check a parameterized form.
(4) Scatter model: I am using the method from Cao et al. 2019; I had run into problems before because I couldn’t reproduce their \(M_*\) versus \(v_{\rm peak}\) plot. In this post I will try this again with the parameterized \(v_{\rm peak}\) function.
Halo \(v_{\rm peak}\) Function
I am using the fit for \(dn/d\ln v_{\rm peak}\) from Appendix A of Comparat et al 2017. This function gives fits for both distinct and satellite haloes, for redshifts \(0<z<2.3\) (note we will need to extend this parameterization to higher redshifts if we want to use it in the abundance matching procedure for the mock catalogues).
The parameterization is (I fixed some typos in their equation):
\[\dfrac{dn}{d \ln v_{\rm peak}} = \dfrac{H(z)^3}{v_{\rm peak}^3} 10^A \left(1 + \dfrac{v_{\rm peak}}{10^{V_{\rm cut}}} \right)^{-\beta} \exp\left[ -\left( \dfrac{v_{\rm peak}}{10^{V_{\rm cut}}} \right)^{\alpha}\right]\]where \(A,\beta,\alpha\) and \(V_{\rm cut}\) are the fitted parameters. I used \(H(0)=70 km /s/Mpc\).
Comparing this to the output from the simulation, I get:
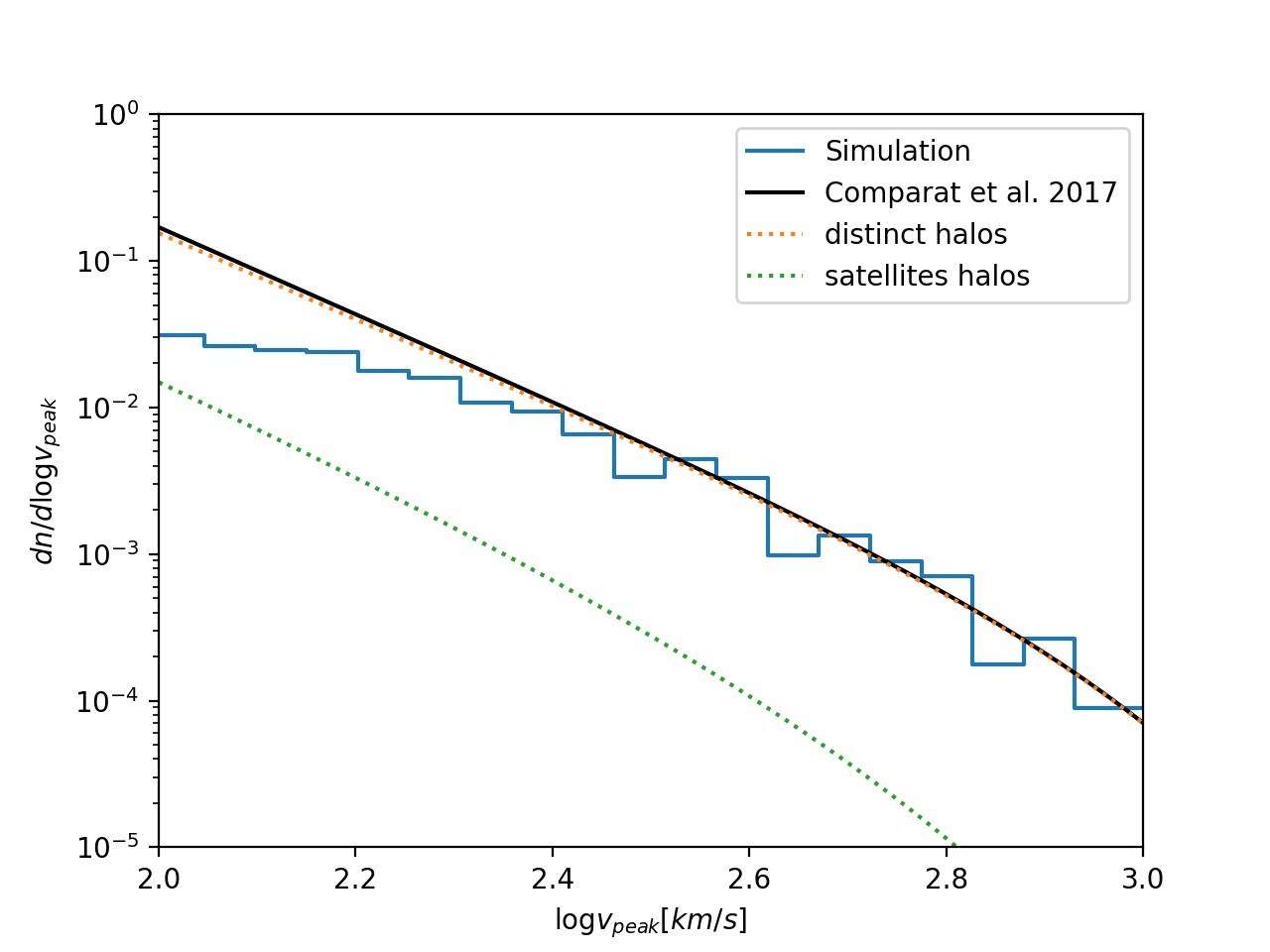
as expected, there are resolution problems below \(v_{\rm peak} \approx 2.6\).
Halo Mass - Stellar Mass Relation
I can now recover the expected relation between \(M_*\) and \(V_{\rm peak}\).
From Cao et al. 2019:
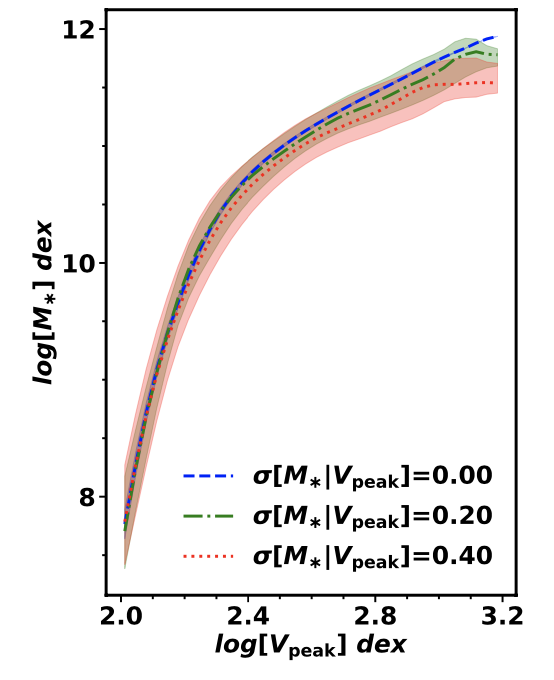
Mine (I also realized I had been missing a factor of \(h^3\) in the stellar mass function…):
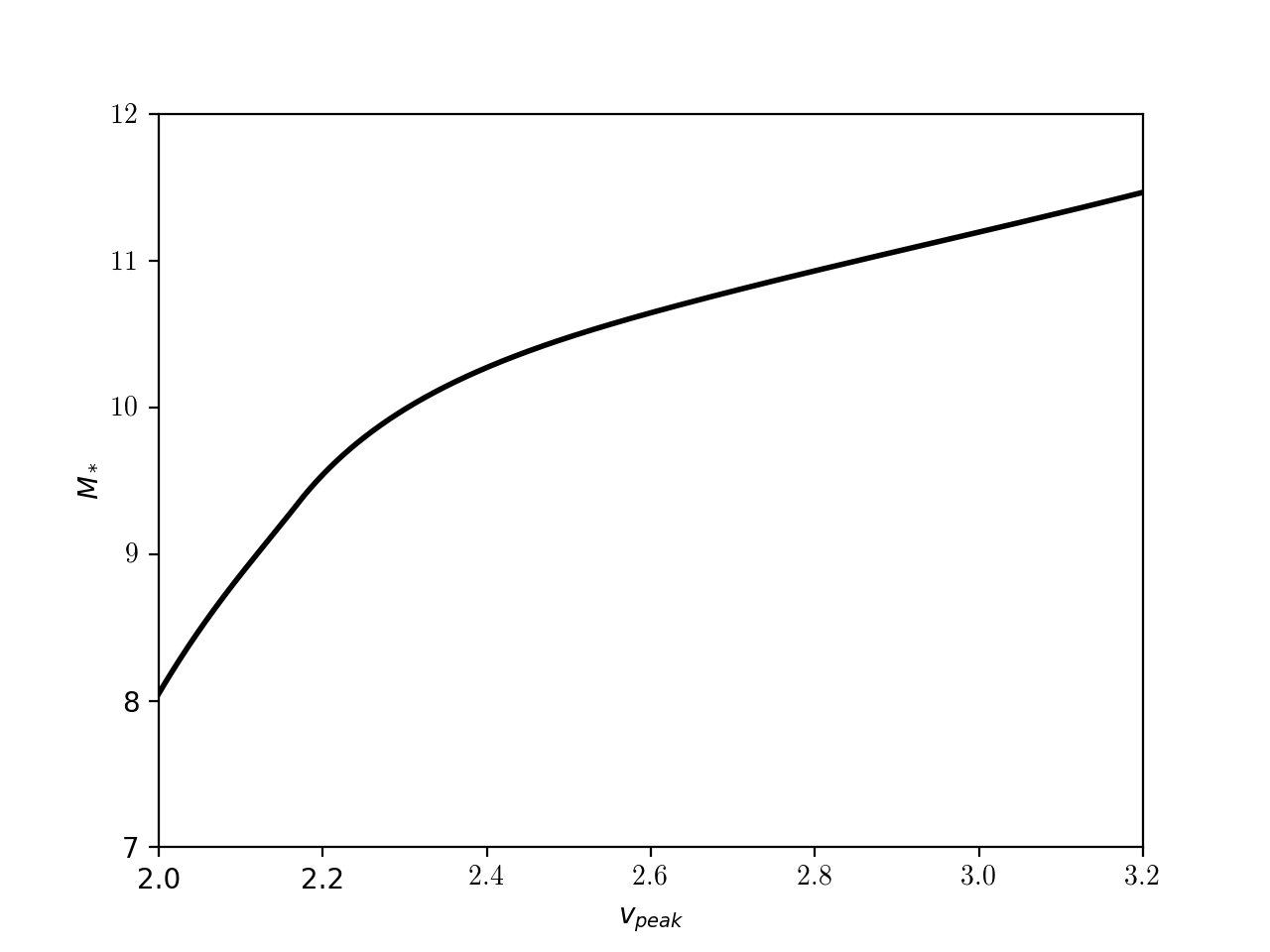
It looks much better! (good enough?)
Scatter Model
And the scatter mapping:
From Cao et al. 2019:
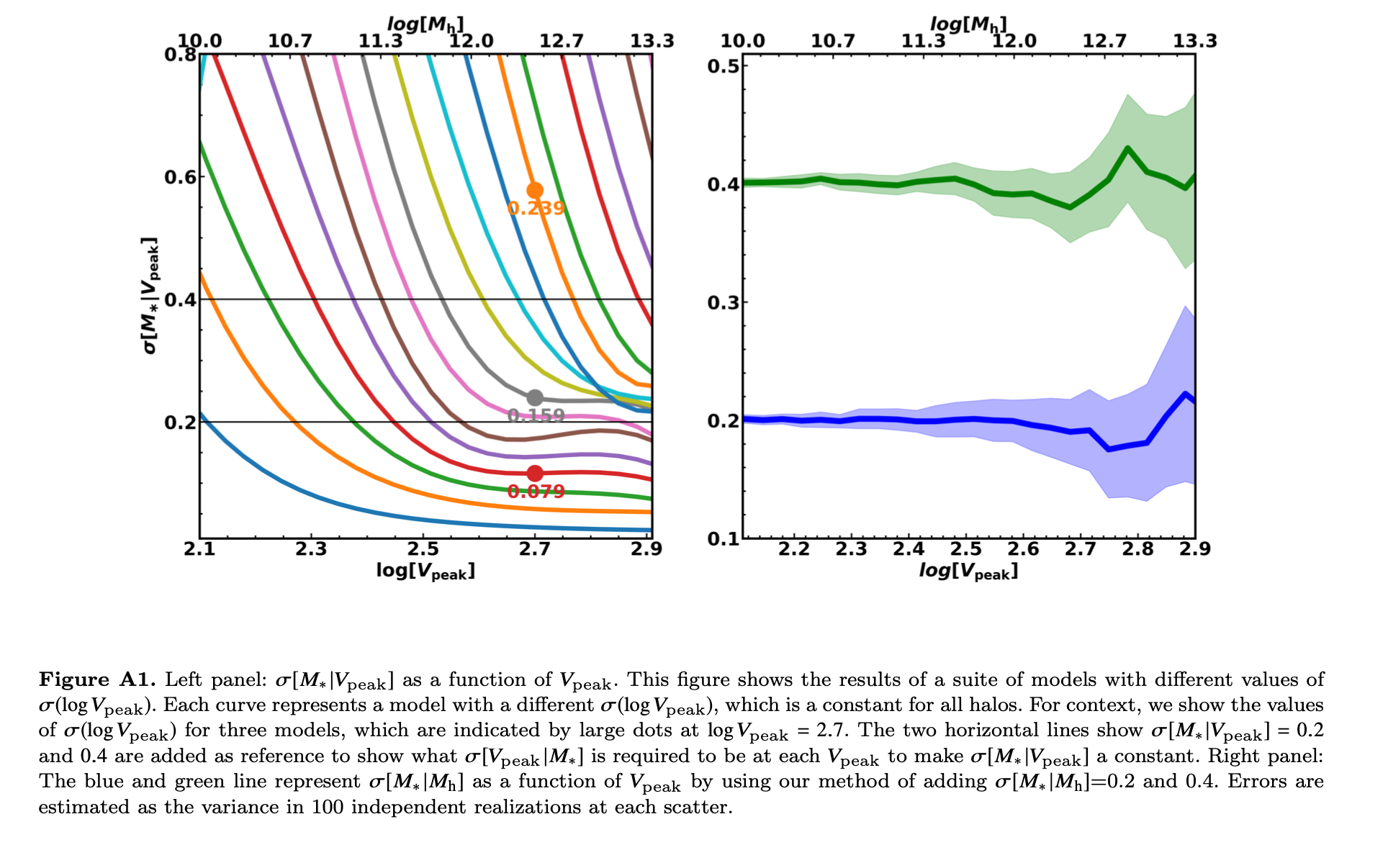
For mine I calculated this by doing the abundance matching for 1000 \(v_{\rm peak}\) values, binning it into 100 bins, and calculating the standard deviation in each. Then I repeated this 1000 times and averaged it to get a smoother relation.
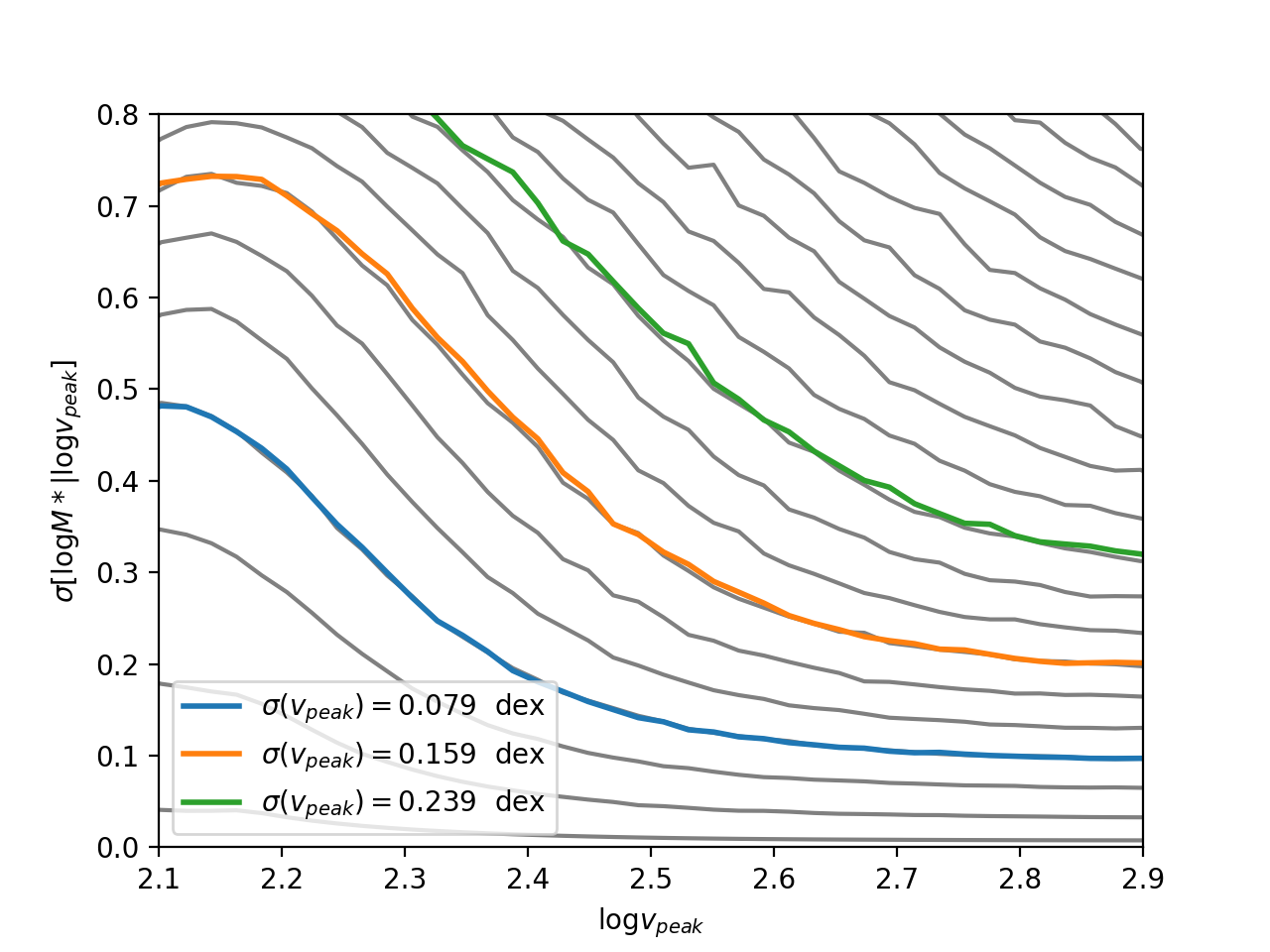
This is a lot better, but still doesn’t match. I will look into this more another day, but for now it seems to be roughly working.
Next In This Project
Now the abundance matching procedure is pretty much ironed out (with the exception of the scatter mapping), at least at \(z=0\). I will finish fixing this, and check that the abundance matching results in the proper stellar mass function with the appropriate scatter.
Then, the next thing I am going to focus on is making a light cone. This will also help us determine what we need for the dark matter only simulation.