Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Testing Neutrino IC Velocities
I have been working IC code with dark matter particles. I also have sorted out how to add neutrinos as a second species. In this post I’ll go through the velocity assignment, and check what they look like in Gadget.
Velocity Assignment
As an overview, neutrinos will be on a coarse grid, \(N_{\rm coarse} \times N_{\rm coarse} \times N_{\rm coarse}\). At each point, the particles with have a bulk velocity given by the local density.
At each point of the grid will have \(N_{\rm shell}\) neutrinos that sample the Fermi Dirac distribution, and for each of these velocities, will have \(12 N_{\rm side}^2\) different directions. Therefore there are \(N_{\rm side} \times 12 \times N_{\rm shell}^2\) neutrinos at every coarse grid point.
Bulk Velocity
I will calculate the bulk velocity the same for the neutrinos as I did for the dark matter, (\(\vec{v} = a \dot{D} \vec{L}\)), where \(\vec{L}\) is the displacement vector. I don’t think this is quite accurate (see my derivations, which I’ve written up separately), but I think it should work well as an approximation. We can look into the affect of this assumption later.
An alternative method is to calculate this from the velocity power spectrum of the neutrinos.
Velocity from Fermi-Dirac Distribution
Luckily, I already wrote code to do this!
Current IC Code
Here is the code that now includes velocity assignments
Distribution of Neutrino Velocities
If I compare the distribution of particle momenta to what’s expected from the Fermi-Dirac Distribution, I find this:
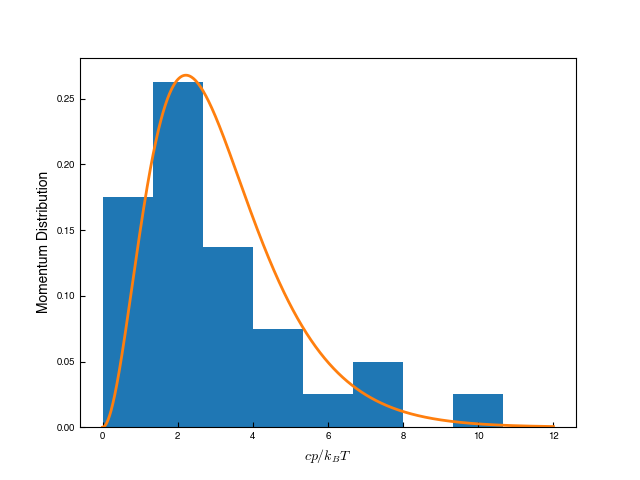
It’s not resolved very well, since this is only with \(N_{\rm shell}\) particles, but it looks reasonable.
Next Step
The next step is to run this in Gadget, and check everything looks okay.