Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Background Ionizing Photons
As discussed in the two previous posts, my reionization bubbles were growing too slowly. It seems that this is due to not accounting for bubble overlap.
I plan to do a correction by accounting for background photons; i.e. \(f_{ esc} \dot{N}_{ion}\) became \(f_{ esc} \dot{N}_{ ion} + \dot{N}_{background}\).
In this post I’m going to summarize the models I’ve tried (some of these were explored in the previous post).
Bubble Fraction Calculation
It is also worth double checking my calculation for what the ionized fraction is!
To calculate the ionized fraction at redshift \(z\), I am taking a slice in the lightcone around \(z\), and considering the bubbles of all those galaxies. That is, I find the cross section of the bubbles’ spheres at precisely redshift 7. Then, I am generating N random numbers in the area of the lightcone at that redshift, and calculating the fraction of random points that lie within a bubble.
Taking a slice in redshift is needed so that the very large lower redshift bubbles don’t extend into the desired redshift. I tried different slice sizes, but this didn’t make a noticeable difference.
I also considered the possibility of edge effects: i.e., there should be galaxies outside the lightcone whose bubbles extend into the lightcone. To account for this, I implemented periodic conditions on the edges. Again, this made very little difference.
For all the plots shown in this post, I used
- A slice of +/- 10 cMpc/h around redshift \(z\)
- 10000 random points
- periodic boundary conditions (on edges of light cone AND in redshift slice)
Models
Model 1
The simplest model is:
\[\dot{N}_{background} = \dot{n}_{\rm ion} V\]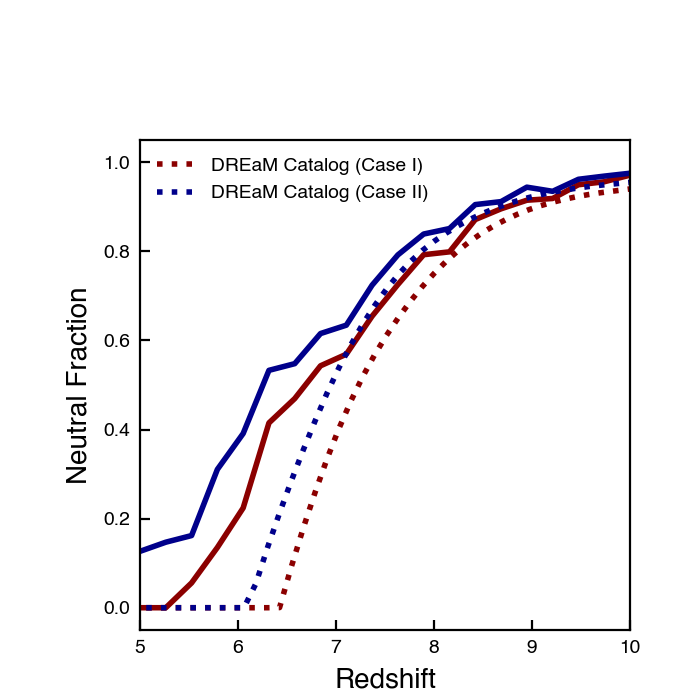
But this doesn’t allow the bubbles to grow quickly enough. I think this is because there is inhomogenities; i.e. a bubble is more likely to be close to other bubbles.
Model 2
In the previous post I tried \(\dot{N}_{background} = \dot{n}_{\rm ion} Q V\), with the reasoning that I expect that bubbles should overlap (on average) with ionized regions of size \(QV\). The bubbles didn’t grow quickly enough with this model, so I also tried adding in a Clumping term (C=3, as used for the recombination term) to account for inhomogenities in the IGM:
\[\dot{N}_{background} = \dot{n}_{\rm ion} Q V C\]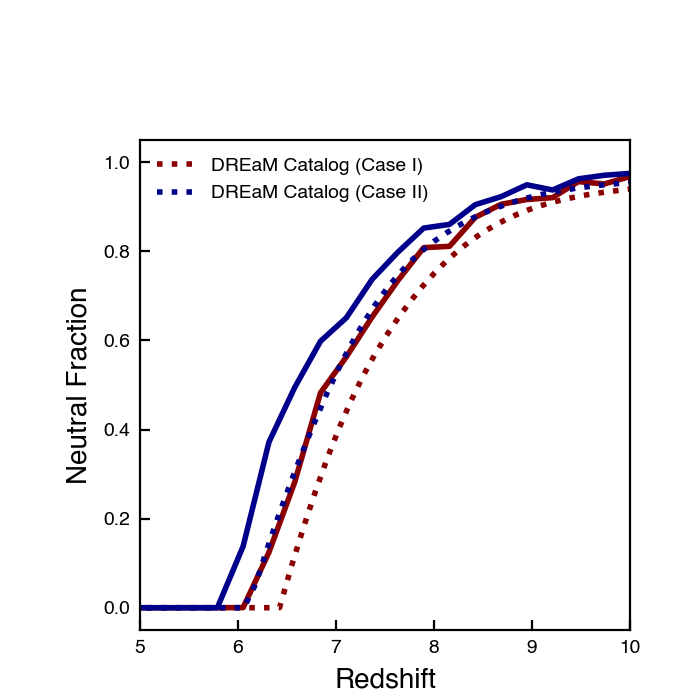
This isn’t too bad, but (1) the bubbles still don’t grow quickly enough and (2) I’m not sure the math makes sense.
Model 3
If I instead frame the problem as:
\(\dot{N}_{background} =\) [rate of photons produced in 1 bubble] \(\times\) [probability of overlapping 1 bubble] +[rate of photons produced in 2 bubble] \(\times\) [probability of overlapping 2 bubble] \(+\) …
If I assume the probability of overlapping with one bubble is \(Q\) (I don’t think this is quite right though; I think Q is the probability it overlaps with AT least 1 bubble), then the rate of photons produced in each bubble is approximately \(\dot{n}_{\rm ion} V\), and the probability of overlapping with \(m\) bubbles is \(Q^m\).
Then,
\(\dot{N}_{background} = \dot{n}_{\rm ion} V \sum (m Q^m)\).
As long as \(Q<1\), \(\sum (m Q^m)\) converges. At \(Q=1\) the bubble sizes are effectively infinite anyway, so that value doesn’t matter. Therefore, I’ll just pick some large number to sum over.
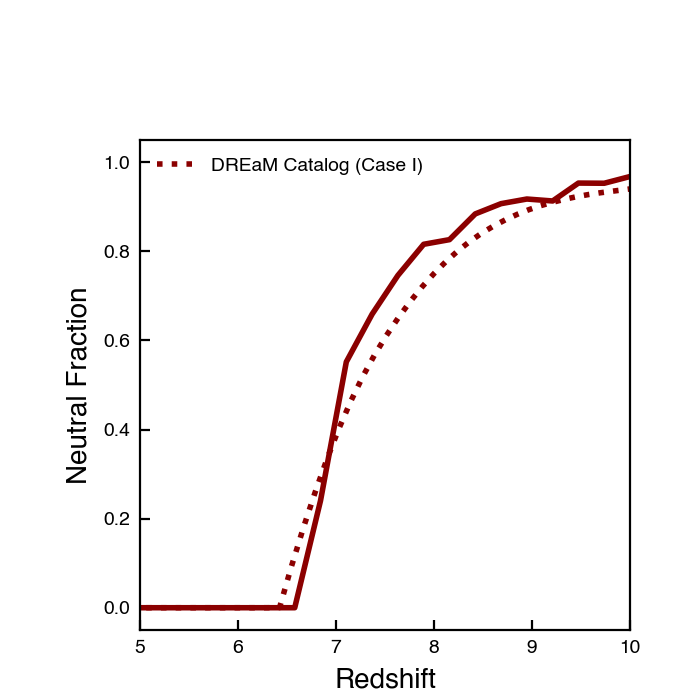
(Note I only plotted Case I, because I messed up Case II, and it didn’t seem worth re-running.)
This is okay, but the bubbles seem to grow too slowly at first, and then grow too rapidly.
Model 4
If I instead consider
\(\dot{N}_{background} = \dot{n}_{\rm eff} V\), where \(\dot{n}_{\rm eff}\) is the effective contribution, and also define some total volume \(V_{\rm tot}\), and the number of bubbles in this volume to be \(N_{b}\).
The volume covered by these bubbles is \(V_b = Q V_{\rm tot}\)
Then,
\[V_b \dot{n}_{\rm ion} = \sum V_i \dot{n}_{\rm eff}\]and if we assume every bubble has the same volume, \(V\)
\[\dot{n}_{\rm eff} = \dfrac{Q V_{\rm tot} \dot{n}_{\rm ion}} {N_b V }=\dfrac{Q \dot{n}_{\rm ion}}{n_b V }\]If we assume that each galaxy produces \(f_{\rm esc }\dot{N}_i\) ions, then
\[\dot{n}_{\rm eff} = \dfrac{Q f_{\rm esc }\dot{N}_i}{V}\]And we can calculate
\(\dot{N}_{background} = Q f_{\rm esc }\dot{N}_i\).
This is actually very similar to Model 2, if you make the assumption \(\dot{N}_i \approx \dot{n}_{\rm ion} V\)
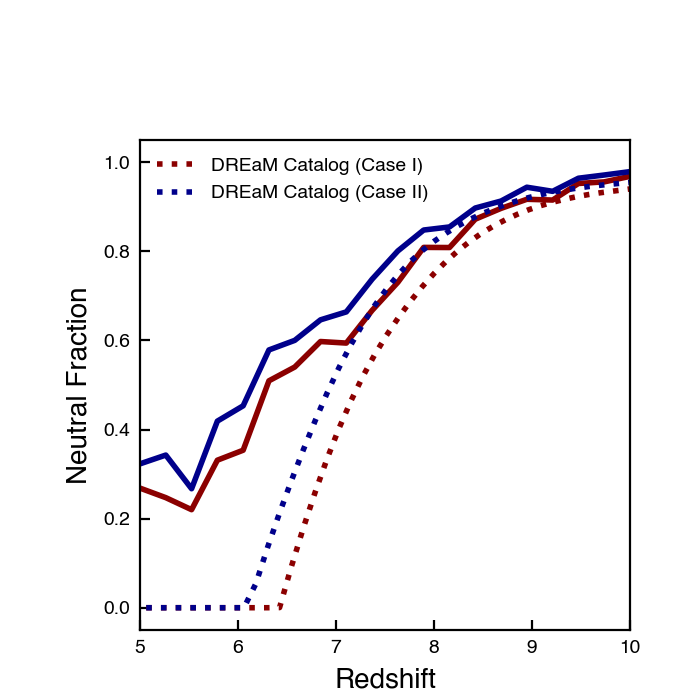
This model looks the worst so far.
Model 5
Going back to Model 1 and 2, I can consider the general form:
\[\dot{N}_{background} = \dot{n}_{\rm ion} V C\]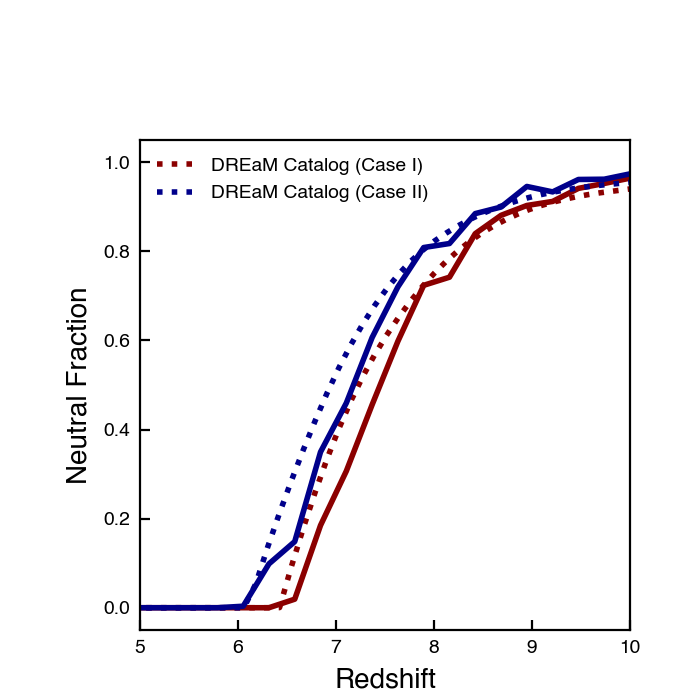
this grows a little too quickly but looks pretty good. However, I don’t think the clumping factor doesn’t really make much sense mathematically here, and is more of a fudge factor.
Model 6
Since \(C=\dfrac{\langle n^2 \rangle}{\langle n\rangle ^2}\), maybe we actually want the square root of this?
\[\dot{N}_{background} = \dot{n}_{\rm ion} V \sqrt{C}\]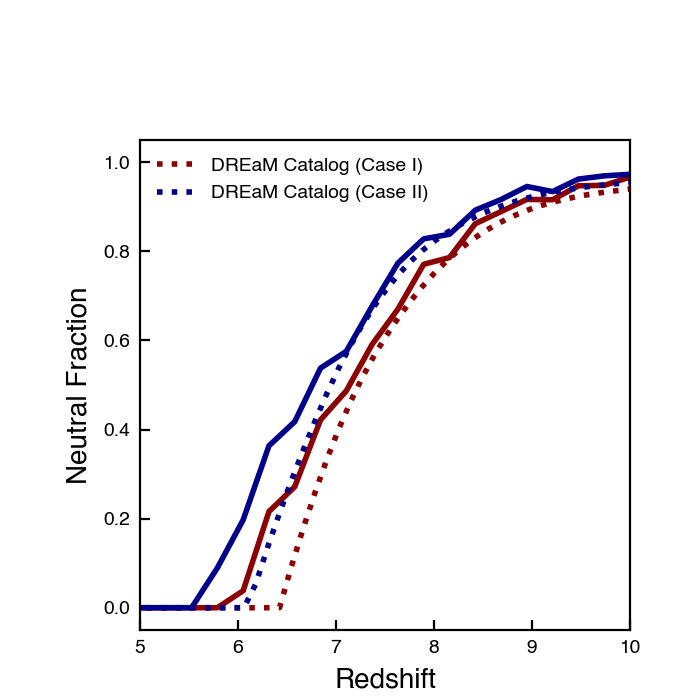
Model 7
Since it looks like the truth is inbetween Model 5 and Model 6, I also tries multiplying by a factor of 2, even though I don’t have an argument for why this would be the case.
\[\dot{N}_{background} = 2 \dot{n}_{\rm ion} V\]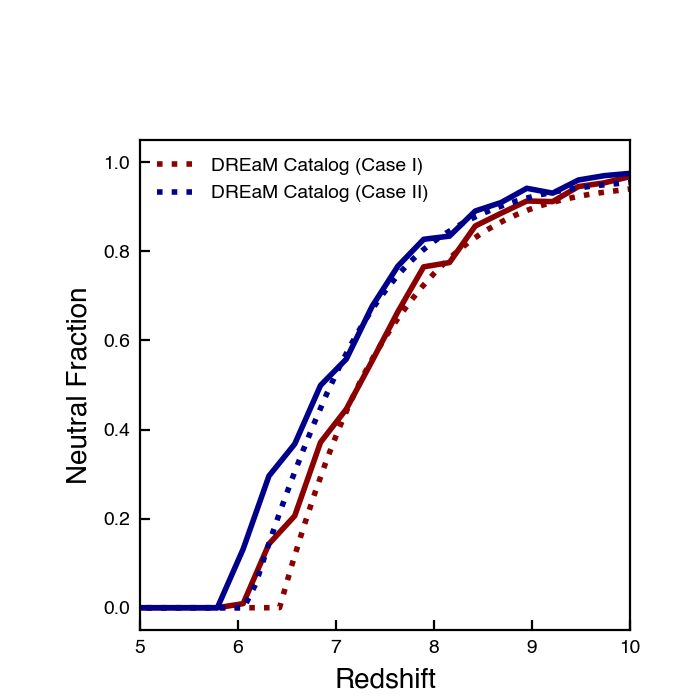
Conclusions
I’m still not entirely sure what to use. So far either Model 6 or Model 7 seems the best. Model 7 is slightly better, but Model 6 has a better physical motivation.
I think I’ll use Model 6, and put a pause on this for now.