Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Tidal Stripping of NGC 1052-DF2
For Bradley’s paper, we want one “realistic” example. So I’m going to set up a simulation for the ultra diffuse galaxy NGC 1052-DF2, guided by the model in Ogiya et al. 2022.
Subhalo Model
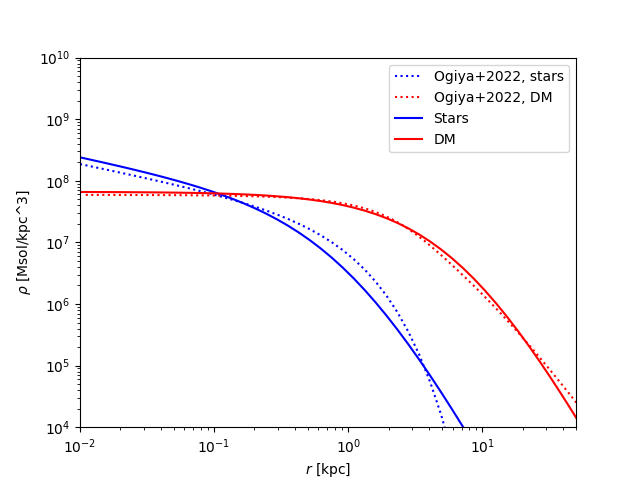
They found that this UDGF was better described by a cored dark matter profile. This was created by modifying an NFW profile (with \(M_{200} = 6 \times 10^{10} M_{\odot}\). \(c = 6.6\), \(z=1.5\)). This corresponds to \(r_s=12.24\) kpc, \(r_{vir} = 80.76\) kpc.
The stellar component was modelled using a Sérsic profile with a stellar mass of \(M_* = 2 \times 10^8 M_{\odot}\), a Sérsic index of \(n=1\), and effective radius of \(R_e = 1.25\) kpc.
For our case, we want to use a double alpha profile (for simplicity).
The stellar component was created with the same total mass and \(\alpha\) parameter. The scale radius was found from finding the peak in \(\log_{10} r^2 \rho\). This corresponds to \(\alpha = 0.44\), \(r_s = 1.10\), and \(\rho_0 = 3.07\times 10^7\).
Our dark matter halo was created with the same scale radius, alpha parameter and virial mass, \(r_s = 6.91\), \(M (6.6 r_s) = 6 \times 10^{10} M_{\odot}\), \(\alpha=0\). This corresponds to \(\rho_0 = 6.62 \times 10^7\), and \(M_{\rm tot} = 9.15 \times 10^{10}\).
Here is a comparison of the model in Ogiya et al. to our model:
Host Model
The Ogiya et al. 2022 paper uses a time-varying NFW potential, and the merger happens from \(z=1.5\) to \(z=0\). I will take the host properties at \(z=0\): \(M_{200}=1.1 \times 10^{13} M_{\odot}\), \(c=6.8\).
Using the critical density in a Plank cosmology at redshift 0, this corresponds to \(r_{\rm vir} = 458.76\) kpc, and \(r_s = 67.46\) kpc
Orbit
Ogiya et al. 2022 uses orbital parameters \(x_c = r_c(E)/r_{200} = 1\), and \(\eta = L/L_c(E) = 0.3\)
If will use an infall radius and velocity of \(458.73\) kpc and \(61.85\) km/s. This corresponds to \(x_c = 1.39\) and \(\eta=0.3\).
Units
Going back to my unit system of \(M_{ sat}=1\), \(G=1\), \(r_{1}=1\), I can put this together as:
IC parameters
alpha1 =0.44
alpha2 = 0.0
r1 = 1.0
r2 = 11.12
M2divM1 = 457.5
Host potential parameters
NFW_Mvir = 120.22
NFW_C = 6.8
SAT_C = 84.5
Orbit parameters
r_orb = 417.03
v_orb = 0.10
This corresponds to an orbital period of \(1950 t_{ unit }\). This is about 10x slower than the other orbits I have looked at, so this might take a while to run.