Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Abundance Matching
In subhalo abundance matching (SHAM), you assume that the abundance of halos as a function of their mass (or some other mass proxy), \(n(x)\) is related to the stellar mass function \(\phi (M_*')\) as follows:
\[\int_x^\infty n(x') {\rm d}x' = \int_{M_*}^\infty \phi (M_*') {\rm d}M_*’\]While there are different mass proxies, \(x\), used in the literature, we will adopt \(v_{\rm peak}\), which is the peak maximum circular velocity, \(v_{\rm max}\), a halo reaches in it’s accretion history. This mass proxy seems to reproduce clustering results better than other quantities (e.g. Campbell et al. 2018). Presumably, \(v_{\rm peak}\) will be equal to \(v_{\rm max}\) at the current redshift for host halos, and equal to \(v_{\rm max}\) at accretion for satellite halos.
Current Method
(1) Get/run a simulation
(2) Run a halo finder and merger tree generator on the simulation (we used AHF)
(3) Measure \(v_{\rm peak}\) for every halo
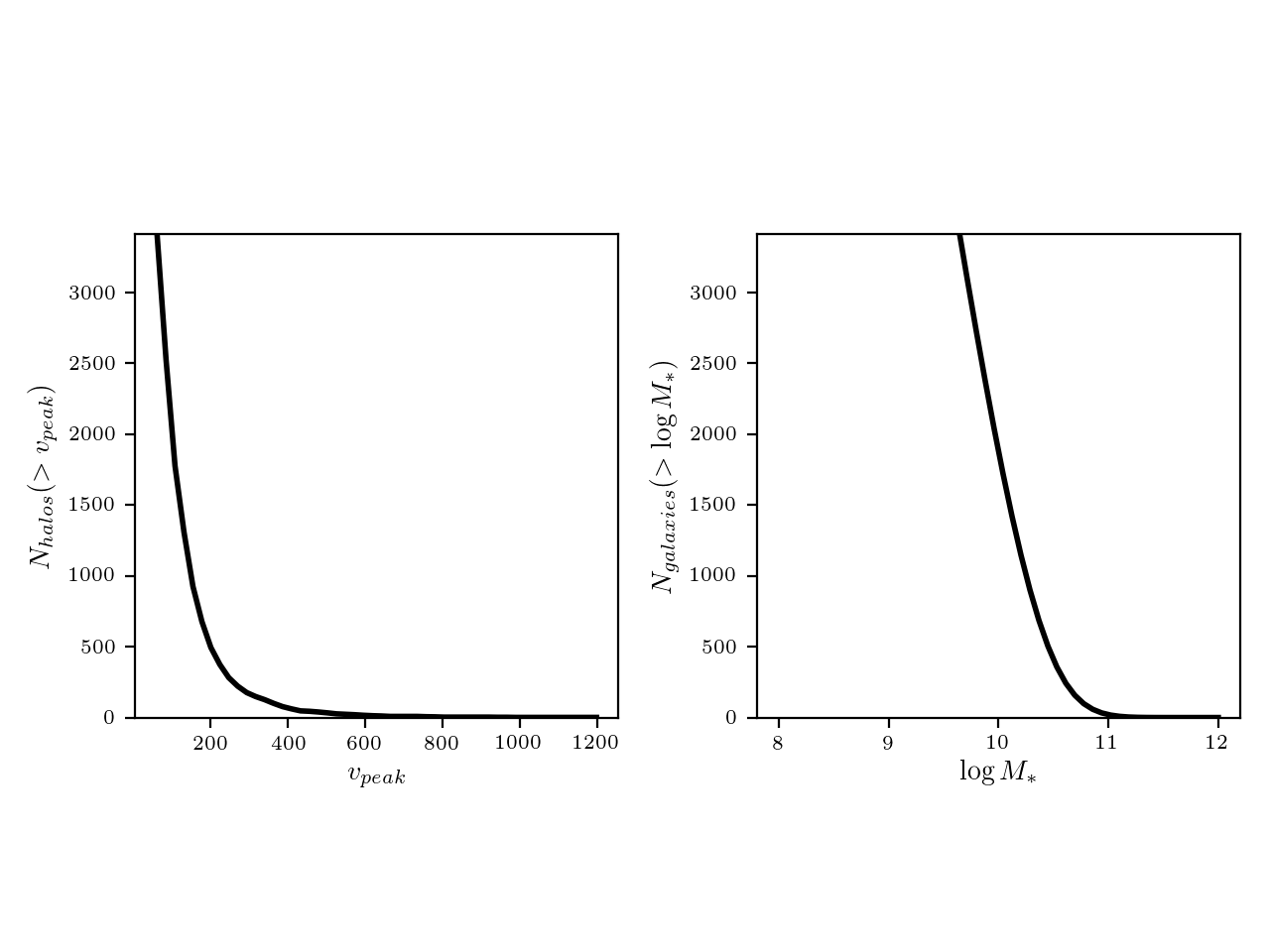
(4) From the simulation, calculate \(N_{\rm halos}(< v_{\rm peak})\)
(5) From a chosen stellar mass function, calculate \(N_{\rm galaxies}(< M_*)= V \int_{M_*}^\infty \phi (M_*') {\rm d}M_*’\), where \(V\) is the simulation volume (note that this assumes that \(\phi (M_{\rm max}) \approx 0\), where \((M_{\rm max})\) is the maximum stellar mass in the parameterization)
(6) Do the abundance matching. Each halo with a given \(v_{\rm peak}\) can be assigned a stellar mass by setting \(N_{\rm halos}(< v_{\rm peak})= N_{\rm galaxies}(< M_*)\)
Test Results
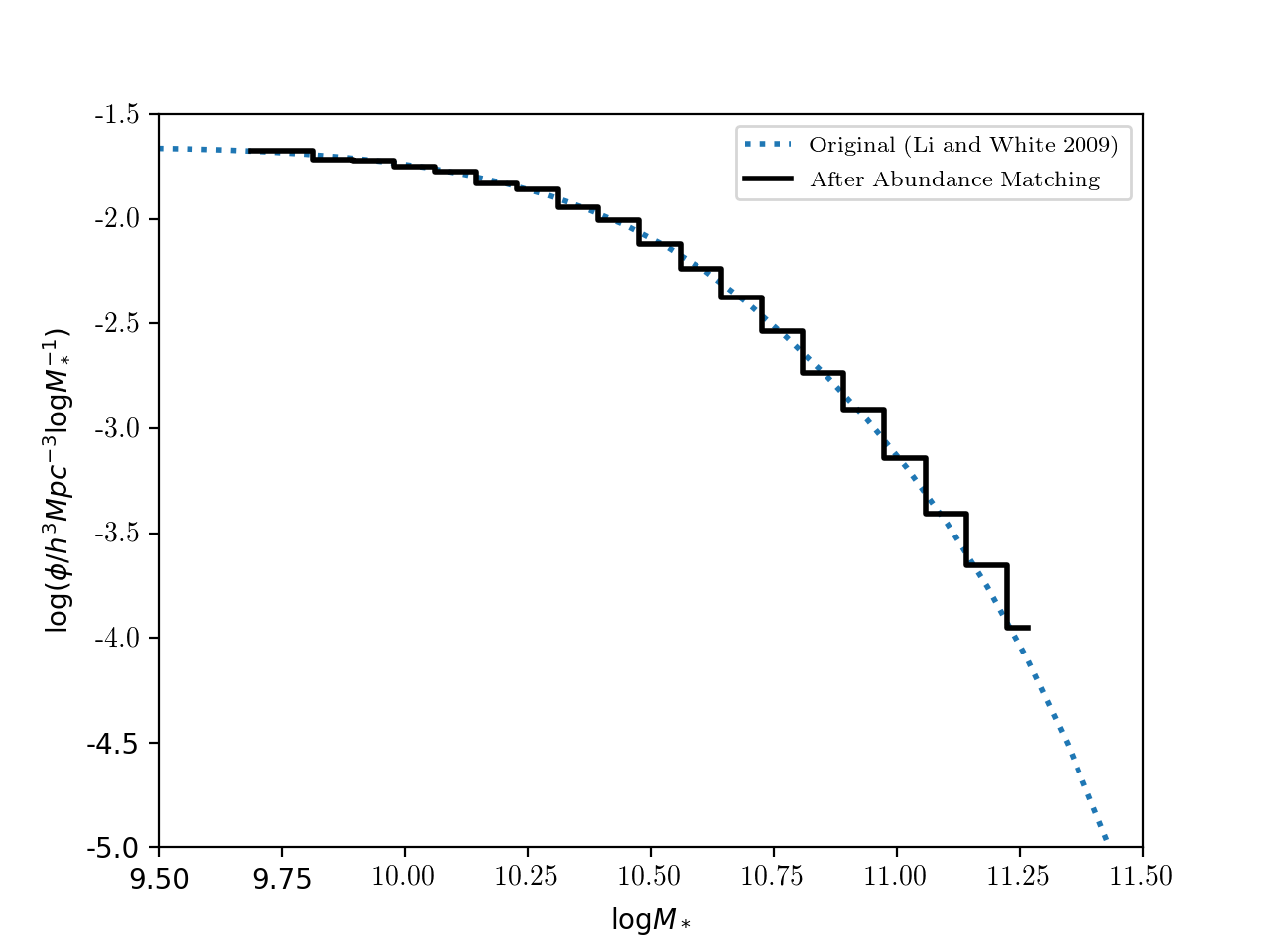
I have tested this with a sample simulation provided by Brant (spergel_2LPT_256). It has \(256^3\) particles and a box size of 60 Mpc/\(h^3\). The SMF was parameterized using Li & White 2009.
Plots showing the calculated number of \(N_{\rm halos}(< v_{\rm peak})\) and \(N_{\rm galaxies}(< M_*)\):
After abundance matching, to recover the SMF, the output galaxy masses were binned, and then divided by the bin width.
What’s Next
While the current implementation has zero free parameters, it does not contain any scatter in the stellar mass – halo mass (SMHM) relation. That will be the topic of the next post.