Abundance Matching 512 Sims

In this post, I am going to do abundance matching on the \(512^3\) simulations at redshift zero. I had sorted out a lot of this before, but there were still some issues (see this post for a summary); some of these issues may have been because of the sample simulation I was using.

Before, I was using the stellar mass function from Li & White 2009 and the halo \(v_{\rm peak}\) function (HVF) from Comparat et al 2017.

Halo Vpeak Function

In my last post, I showed that the halo mass function (HMF) of the \(512^3\) agrees with the expected curve. I also want to check the halo \(v_{\rm peak}\) functions from the simulation look right.

I am using the halo \(v_{\rm peak}\) function (HVF) from Comparat et al. 2017. When I compare their parameterization to the distribution from the simulation I get:

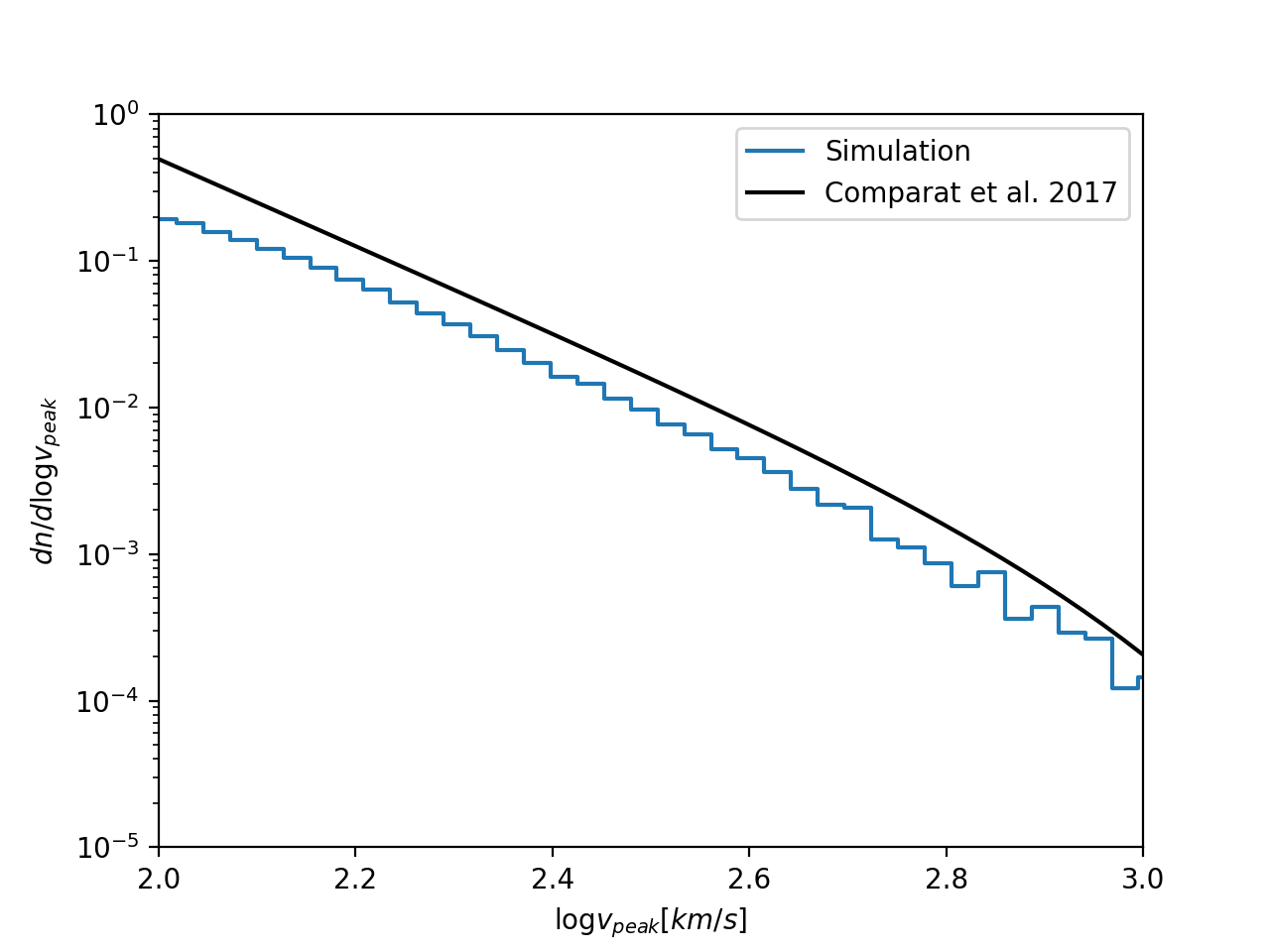
The two curves don’t agree… It possible I am doing something wrong (I already found two typos in the parameterization from Comparat et al 2017. Another possibility is that the discrepancy is because the parameterization was calibrated from a different cosmology, using a different mass definition in their halo finder (virial SO). However, since their parameterizations only goes to redshift 2.3, I won’t be able to use it anyway. Therefore, I am not going to worry about it right now.

Abundance Matching (No Scatter)

The basic method for abundance matching is to solve for the galaxy mass, \(M_*\), of each halo, given their peak circular velocity \(v_{\rm peak}\), using the equation:

\[\int_{v_{\rm peak}}^{\infty} n(v_{\rm peak}') {\rm d}v_{\rm peak}' = \int_{M_*}^{\infty} \phi(M_*') {\rm d}M_*'\]

Note that the HVF and SMF are only defined out to some maximum mass/peak velocity. Therefore, I am integrating out to the maximum \(v_{\rm peak}\) and \(M_*\) values defined in the parameterizations. I am hoping that \(n\) and \(\phi\) are small enough outside these values that it won’t influence the results much; however this could alter the \(M_*\)–\(v_{\rm peak}\) relation. I need to check how sensitive the results are to this truncation in the integrals.

I am using the HVF, \(n(v_{\rm peak})\), measured from the simulations. As before, I am using the SMF, \(\phi(M_*)\), from Li & White 2009 (this will eventually have to be extended/updated for higher redshift, but will serve to test that the abundance matching procedure is working).

After performing the matching procedure, and checking the recovered SMF:

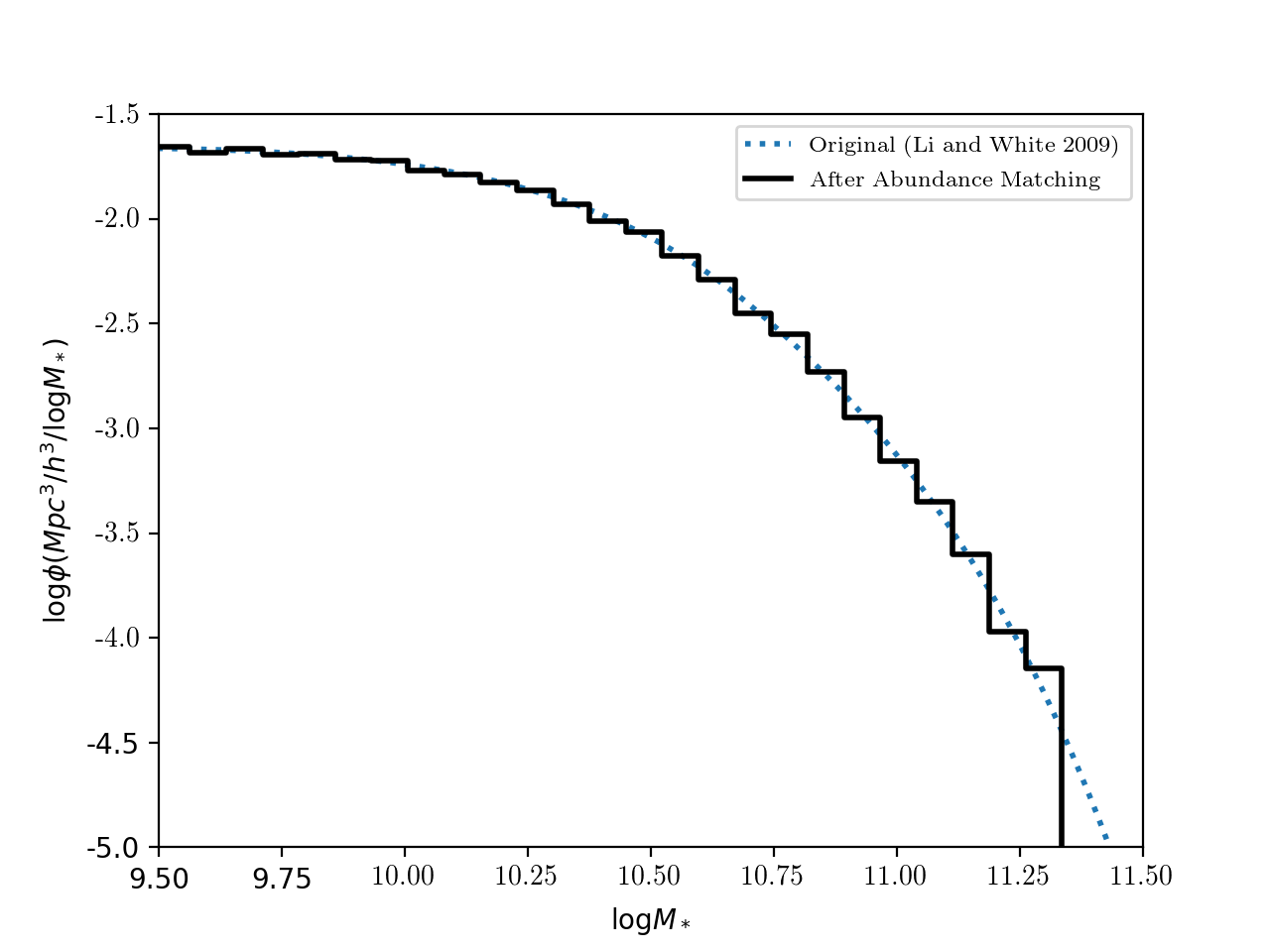
This looks good!

\(M_*\) versus \(v_{\rm peak}\)

From the abundance matching procedure, we can obtain the relation between galaxy mass, \(M_*\), and the halo mass proxy, \(v_{\rm peak}\):

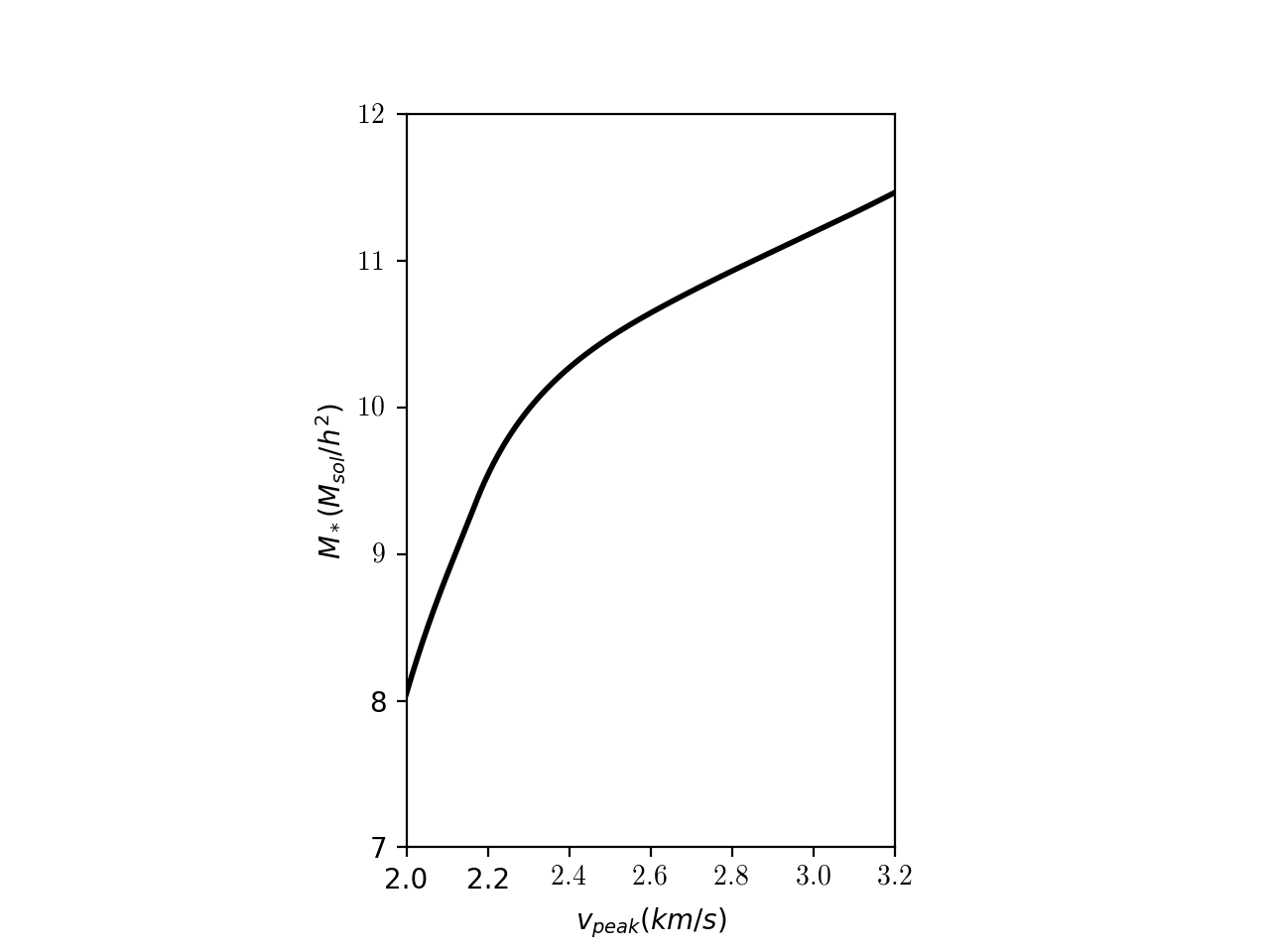
Note that this doesn’t match the plot from Cao et al. 2019:

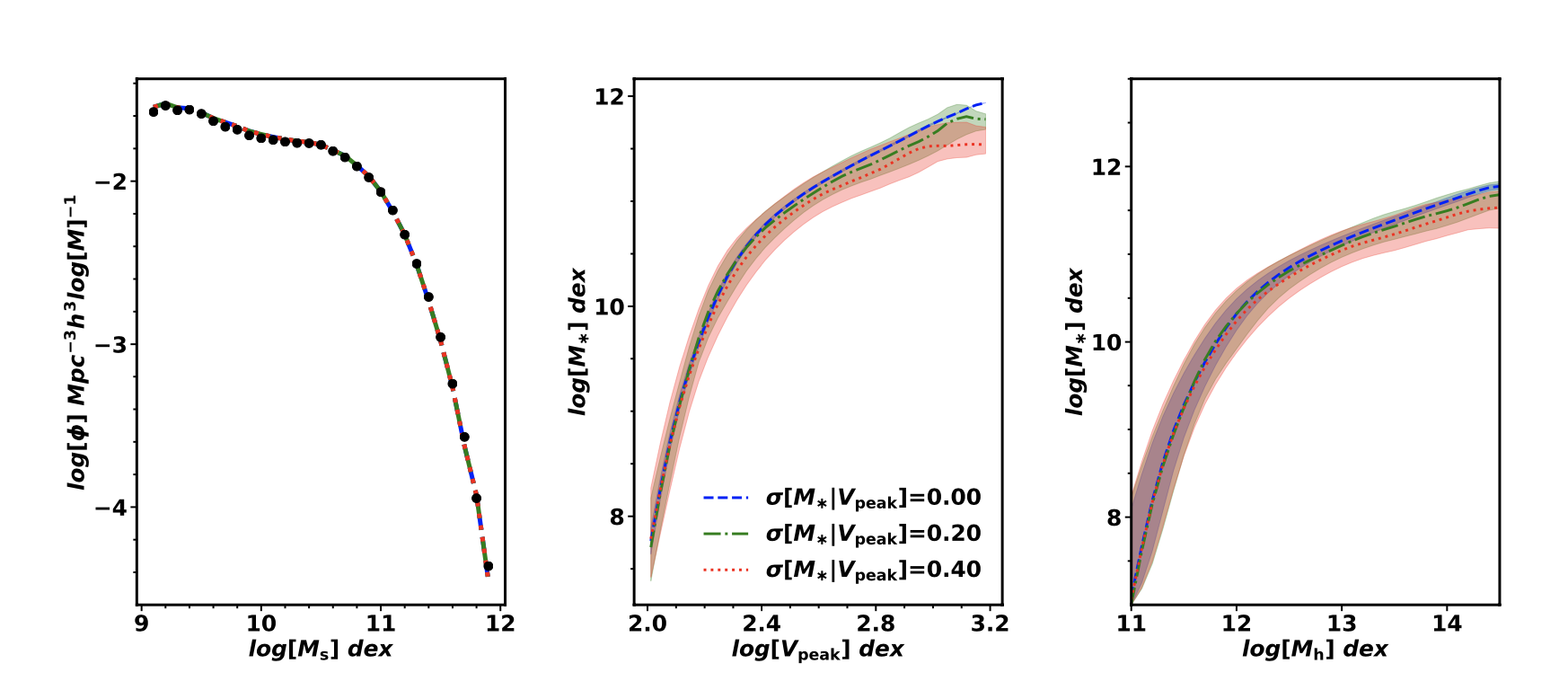
This was something I looked into before, and now I think the reason it doesn’t match is that my stellar mass function looks different than theirs. I am also not sure how many factors of \(h\) are in the mass units of the plot from Cao et al. 2019, though this just shifts the curve vertically by a factor proportional to \(\log_{10}(h)\). It is also possible that the discrepancy is because of how I am truncating the integrals in the abundance matching procedure.

I did plan on updating the SMF eventually; therefore I am going to focus on this next, and see if this fixes the discrepancy in the \(M_*\)–\(v_{\rm peak}\) relation.

Scatter in Abundance Matching

I decided to do the procedure for introducing scatter presented in Cao et al. 2019, as outlined in an earlier post. Briefly, the scatter in galaxy masses appears to be roughly constant, but in the abundance matching procedure it is easier to add scatter to the \(v_{\rm peak}\) values. Therefore, the method involves adding constant scatter to \(v_{\rm peak}\), and mapping out the relation between \(v_{\rm peak}\) scatter and \(M_*\) scatter as a function of mass; then for a given halo, you can choose the amount of scatter to add to \(v_{\rm peak}\) to give the desired scatter in \(M_*\).

In the earlier post, I couldn’t tell if my procedure was working, since I couldn’t reproduce the scatter relation from Cao et al. 2019. However, I think that this was because I had a different \(M_*\)–\(v_{\rm peak}\) relation. Therefore, I plan on sorting out that issue first, and then I will revisit the scatter model.

Next Steps

1. Update the SMF, and extend it to higher redshift, following Williams et al. 2018.

2. Check how sensitive the results are to the truncation in the integrals in the abundance matching procedure.

3. Check if the scatter model works with the updated \(M_*\)–\(v_{\rm peak}\) relation

4. Decide whether I want to fit a parameterization to my HVF (since I may run into issues when the values are scattered outside of simulation range during the scatter step of the abundance matching procedure—though I might just be able to truncate at some mass that is within the range of the simualtion).

---

« Light Cone 512 Sims

Stellar Mass Functions 2 »