Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
FSPS UV Properties
We want to match the FSPS SEDs to galaxies based on their UV magnitude and UV continuum slope (see this post for an overview). I will refer to these values as the “target parameters”
In this post, I outlined some of the potential free parameters in FSPS.
Fixed Parameters
Some of the “free” parameters will actually be fixed
zred – redshift of galaxy
tage – age of the galaxy (Gyr), in terms of cosmic time. This can be set to the age of the universe at redshift zred
gas_logz – I will set this to be the same as the metallicity logzsol
sf_trunc – This is the time at which star formation turns off. I might play around with this for quiescent galaxies, but for now I am only considering star-forming, so I will leave this to 0.0 (which assumes that star formation is ongoing).
Fixed Parameters
However, the following parameters will be explored:
logzsol – the metallicity. Williams et al. used a range of [-2.2,0.24].
sf_start – start time of SFH, in Gyr. A reasonable range for this is between 30 Myr and tage.
tau – this is the e-folding time in Gyr for star formation; the delayed tau model defined the star formation history as \(\psi(t) \propto t \exp (-t/\tau)\).
FSPS allows values for tau to be in the range [0.1,1e2]. Williams et al. asserts that the maximum allowed should be \(\log_{10} \tau_{\rm max} = 10^{1.11 \log(sf_{start})-2.02}\) (in units of years), to ensure reasonable sSFRs.
dust2 – dust attenuation, in units of \(\log_{10} (yrs)\). Williams uses a range range of [0,4] for \(\hat{\tau}_V\); I am going to use this for now, but I need to check whether these dust parameters are defined the same.
gas_logu – gas ionization parameter. Williams et al. uses a range of [-4,-2].
Creating SED
I’m going to consider a galaxy of mass \(10^8 M_\odot\) at redshift zero. The age of the universe should be about 13.8 Gyr, which sets tage=13.8
For the potential free parameters, I assign them baseline values of logzsol=0, sf_start=10, tau = 1, dust2=0, gas_logz=-2
Here is the code for creating an sps object with my current parameters
sps = fsps.StellarPopulation(zcontinuous=1)
myzred = 0 #redshift
mymass = 1e8 #stellar mass
mylogzsol = 0 #metallicity [-2.2,0.24]; Williams
mytau = 1 #efolding time of star formation (Gyr)
mysf_start = 10 #start of SFH (Gyr)... has to be less than tage
mydust2 = 0 #dust attenuation [0,4]?
mygas_logu = -2 #gas ionization [-4,-2]; Williams
mysf_trunc = 0 #end of SFH (Gyr)... 0 means no truncation
mygas_logz = mylogzsol # gas metallicity
mytage = 13.8 #age of galaxy in Gyr
sps.params['imf_type']=1
sps.params['sfh']=4
sps.params['dust_type']=2
sps.params['add_neb_emission']=True
sps.params['dust1']=0
sps.params['zred']=myzred
sps.params['tage']=mytage
sps.params['logzsol']=mylogzsol
sps.params['tau']=mytau
sps.params['sf_start']=mysf_start
sps.params['sf_trunc']=mysf_trunc
sps.params['dust2']=mydust2
sps.params['gas_logu']=mygas_logu
sps.params['gas_logz']=mygas_logz
FSPS normalizes the star formation history by one stellar mass. The final galaxy mass is stored in the variable sps.stellar_mass. Therefore I scaled the SED luminosity by \(M_{\rm gal}/\)sps.stellar_mass. Note that I am currently including the mass from stellar remnants in sps.stellar_mass. I can turn this off with a flag. I need to think about how the stellar mass functions I used for abundance matching are defined, and whether this should be included.
Additionally, the output of FSPS is in units of \(L_\odot/Hz\). If we consider the object to be 10 parsecs away, we can divide this by \(4 \pi (10 {\rm pc})^2\) to get a flux density, corresponding to the absolute magnitude.
Here is the SED for this example:
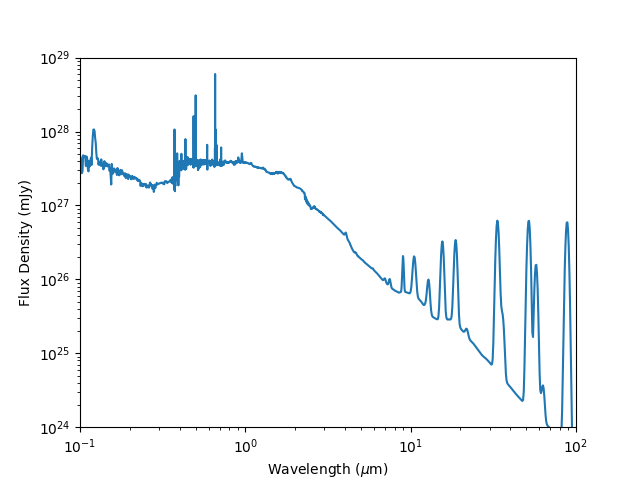
Target Parameters
UV Magnitude
I used the definition of \(M_{UV}\) from Robertson et al 2013: this is the average magnitude at rest-frame wavelength in a flat filter, in range \(1450-1550\) Angstroms.
I calculated the average flux density between the corresponding frequencies (\(\nu_1\) and \(\nu_2\)) as:
\[\langle f_\nu \rangle = \dfrac{\int_{\nu_1}^{\nu_2} f_{\nu}d\nu}{\nu_2-\nu_1}\]Then, the AB magnitude can be calculated from this.
UV Continuum Slope
The UV continuum slope can be measured from the spectrum \(f_\lambda \propto \lambda^{\beta}\). Using eq 2 from Dunlop et al 2012, you can measure \(\beta\) as:
\[\beta = 3.91(Y098-J125)-2\]I calculated the magnitudes in these filters using the builtin magnitude function in FSPS; I used the included ‘wfc3_ir_f098m’ and ‘wfc3_ir_f125w’ filters.
Conclusions
With the parameters above, I get a magnitude of \(M_{\rm UV}=-14.09\) and \(\beta=-1.9\).
These numbers seem reasonable. The next step is to vary the free parameters and see how they influence the target parameters. This will guide how I decide to do the spectrum fitting.