Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Fit HVF
I plan on fitting the halo \(v_{\rm peak}\) function from the simulations to use in the abundance matching step. Here is my set-up for the \(512^3\) simulations (I will have to update this with the higher resolution simulations)
Functional Form
I am following the functional form from Comparat et al 2017 (originally from Rodriguez-Puebla et al. 2016):
\[\log_{10} \left[ \dfrac{v_{\rm peak}^3}{H(z)^3} \dfrac{dn}{d \ln v_{\rm peak} }\right] = \log_{10} \left[ A \left( 1+ \dfrac{v_{\rm peak}}{v_{\rm cut}}\right)^{-\beta} \exp \left[ \left(-\dfrac{v_{\rm peak}}{v_{\rm cut}} \right)^{\alpha} \right] \right]\]There are four parameters to fit \(A\), \(v_{\rm peak}\), \(\alpha\) and \(\beta\). I will use velocity units of km/s and have \(H(z)\) in units of km/s/Mpc. The number density, \(n\) is in \({\rm Mpc}^{-3}\)
As in Comparat et al 2017 I will also consider distinct and satellite halos separately. Each parameter can be expressed as a polynomial in redshift \(p(z)=p_0 + p_1 z + ...\)
Fit at redshift zero
First, here is the fit for the final snapshot, using all the halos with \(\log_{10} v_{\rm peak}>2.2\)
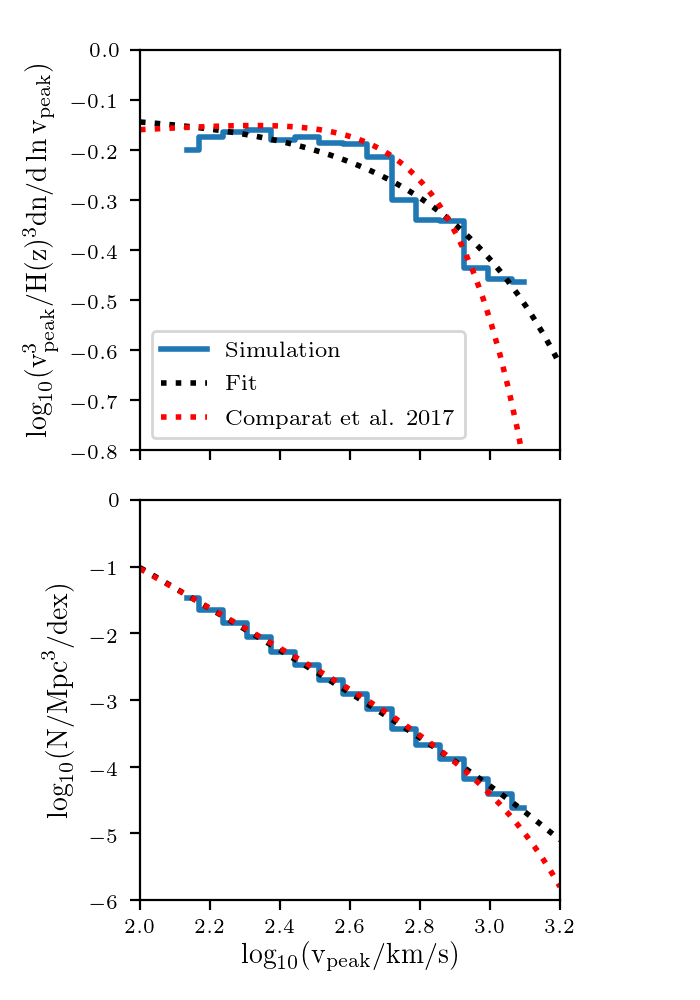
Looks like it is working pretty well (clearly it will be better with the higher resolution simulations).
Redshift trends
Next, I will look at how the four parameters vary with redshift… I will need to calculate \(v_{\rm peak}\) for the halos in each snapshot. Currently I have a script to do this on a single snapshot, by reading in halo catalogs, and using the merger trees to find \(v_{\rm max}(z)\). I will work on automating this to run on all the snapshots.