Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Galaxy Sizes Part II
This is a continuation of this post.
I had problems reproducing W18 trends. Additionally, they used Shibuya for redshifts greater than 4, which depends on UV luminosity. Unlike W18 I am not setting the UV luminosity specifically, and instead recover this information after I have calculated SEDs for each galaxy. Since the the dust attenuation parameter in the SED generation depends on size, I need to calculate size before I get the UV luminosities.
Therefore, I am going to do something a little different than W18, taking advantage of the fact that I have halo properties for each galaxy.
Model
Redshift 0
I will use the findings from Zanisi et al. 2020 for redshift zero. They explore a few different models, but I will use the simple scaling law based on Kravstov et al. 2013:
\(R_e = A_k R_h\) with a lognormal scatter of \(\sigma_K\)
Here, \(R_e\) is the (projected) half-light radius and \(R_h\) is the halo virial radius (Bryan & Norman 1998 definition; virial overdensity with respect to background density).
The \(A_k\) coefficent is given in Table 1 for late type galaxies (LTGs), and Table A1 for early type galaxies (ETGs) The scatter, \(\sigma_K\) is given in Fig. 6 for LTGs and Fig A1 for ETGs.
Higher Redshift
Ma et al. 2018 explores shape relations at higher redshifts using simulations. They find the size of galaxies at fixed stellar mass evolves as \((1+z)^{-m}\), with \(m\approx 1-2\). The value of \(m\) depends on the redshift and mass.
My implementation
I will use the Kravstov relation, but allow a \(z\) dependance as follows:
\(R_e = A_{K,0}(1+z)^{-m} R_h\).
For now I will set \(m=1\), though the relationship is likely more complicated. I will also scale the scatter as \(\sigma_K = \sigma_{K,0}(1+z)^{-m}\).
Then, I will use \(A_{K,0}\) and \(\sigma_{K,0}\) from the \(z=0\) values found in Zasini et al.
Results
Here is the plot from Williams et al (their Fig 15):
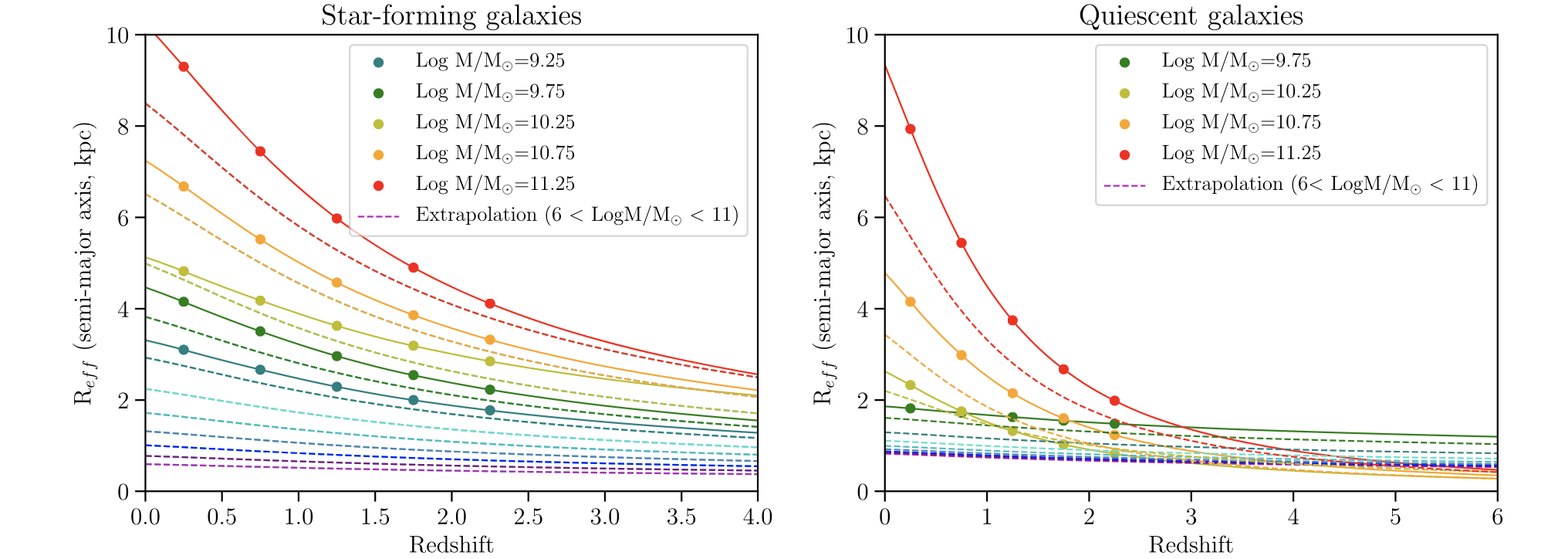
Here is the mean \(R_e\) relation versus redshift for our model. Right now, the halo catalog has defined virial radius as 200 times the critical density (In the current Rockstar implementation that I am updating to, we will switch to the Byran and Norman definition). Since \(\rho_b = \Omega_M \rho_{c}\), I will estimate the difference in the virial radius by multiplying our virial radius by \(\Omega^{1/3} \approx 1.5\).
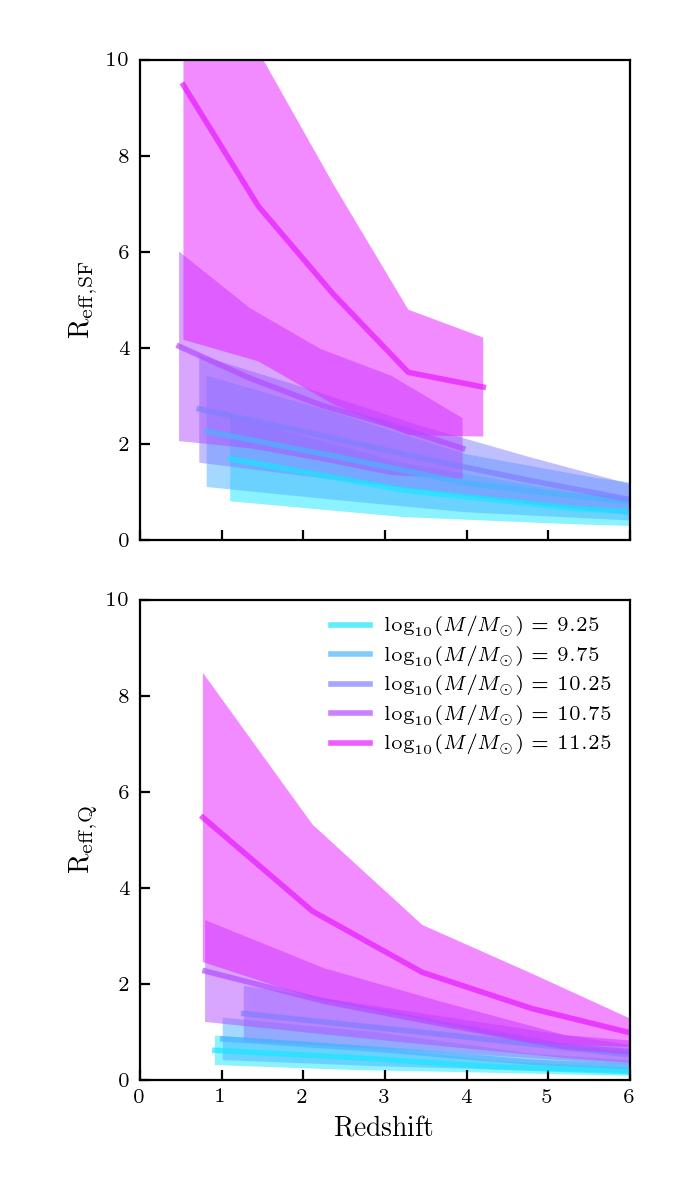
This is in pretty good agreement with the W18 model!
Eventually, I will look through the Shibuya data, and also other references in W18, and plot the data overtop to see if it is consistent with our model.