Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
HMF Lightcone Part II
In my last post, I wanted to check if the HMF recovered from my lightcone looked right. In the last post, I didn’t properly account for the redshift range in the theoretical curve (since the halos are binned in redshift). In this post I fix that, and also think a bit more about whether the recovered HMF is okay.
Fixed Theoretical Prediction
To get the HMF between redshifts \(z_{i}\) and \(z_{i+1}\), I calculated
\[{\rm HMF}(M,z_i<z<z_{i+1}) = \dfrac{\int_{z_i}^{z_{i+1}} {\rm HMF}(M,z'){\rm d}z'}{z_{i+1}-z_i}\]Which gives the following:

Low Mass Issues
I seem to be missing some of the low mass halos at all redshifts.
In this post I had listed some assumptions/possible problems with the implementation I had at the time.
Previously, I was not counting halos that don’t have a progenitor; since I am interpolating positions between snapshots \(j\) and \(j+1\) to find when a halo crosses the backwards light cone, if a halo in \(j+1\) doesn’t have a progenitor in snapshot \(j\), it can’t cross the light cone, and won’t be in the survey. I am guessing this will mostly affect low mass halos.
I have now accounted for these halos by extrapolating for their positions at redshift \(j\), and here is my recovered HMF:
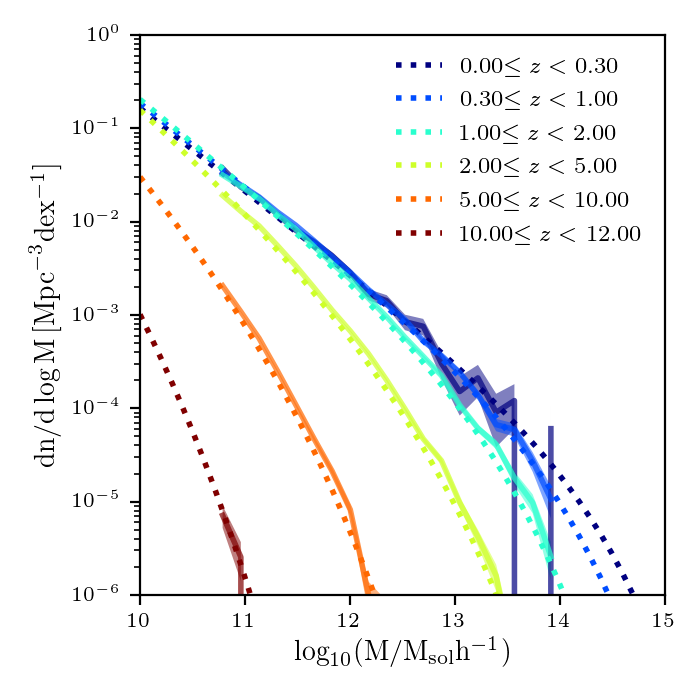
which looks great!
Other Potential Problem: Periodic Boundary Conditions
One thing I realized while adding in the extrapolation, is that I am not accounting for the periodic boundary conditions. Given a halo was at position \(r_j\) in snapshot \(j\) and position \(r_{j+1}\) in snapshot \(j+1\), I am assuming it travelled between these two positions, and not allowing for it to have arrived in the new position by travelling through the simulation box. This might not be too much of a problem, since I have so many snapshots, halos probably rarely pass through the box. However, I do want to fix it.
I will correct the progenitor halo positions by:
\[r_{j} \rightarrow r_{j} - {\rm boxsize}\left( \dfrac{ {\rm sign}(v_{j}) - {\rm sign}(r_{j+1} - r_j) }{2} \right)\]This will ensure that, e.g. if there is a positive \(x\) velocity, the \(x\) position will increase between snapshots \(j\) and \(j+1\). The positions of the progenitor halos are now potentially outside the simulation box.
Then, once I have found where the halo has crossed the lightcone, \(r_e\), I can make sure the periodic boundary conditions are implemented by:
\(r_e \rightarrow r_e \% {\rm boxsize}\).
I am still assuming that a halo will never travel more than a distance of \(\rm boxsize\) (i.e. it never traverses the box more than once between snapshots). I think this is a very reasonable assumption.
Update: this didn’t work well, because the halos would often change velocity directions between snapshots. Instead, to correct the progenitor positions, I used the difference between the extrapolated \(r_j\) and actual \(r_j\) position, \(\Delta r_j\) as follows:
\(r_{j} \rightarrow r_{j} + {\rm int}(\Delta r_j/{\rm boxsize}) \times {\rm boxsize}\)