Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Halo Lightcone Catalogue
Previously, I created a lightcone from AHF halo catalogues, consisting of 3D positions and redshifts for each host halo, in a box of of \((x,y,z) = (60\times115,115,115)\, {\rm Mpc/h}\).
In this post, I outline my method for including subhalos, and also cutting out a wedge that corresponds to the survey volume.
Subhalos
To find the positions and velocities of each host halo as they cross the light cone, I interpolated their positions between snapshots. However, I did not do the same thing with the subhalos, because I was worried that interpolating positions and velocities for the subhalos might cause them to be off-set from their host halos in an unphysical way.
I have added in the subhalos as follows: assuming that a host halo crossed the light cone between snapshots \(j\) and \(j+ 1\), I found all the subhalos in that host halo at snapshot \(j+1\). I then placed these subhalos in the host, and gave them same offset in position and velocity from their host that they have in snapshot \(j+1\).
Note that currently we are taking the properties of the halo at snapshot \(j+1\) (i.e. substructure, mass, maximum circular velocity, shape, spin, and whatever we may need). Later we might use some other criteria to decide whether to take properties from \(j\) or \(j+1\).
Survey volume
First, I converted the comoving \((x,y,z)\) positions of each (sub)halo to an angular position. Following Bernyk et al. 2016, I calculated a distance, RA and Dec for each halo as follows:
\[d = \sqrt{x^2 + y^2 + z^2}\] \[{\rm RA} = \arctan(y/x)\] \[{\rm Dec} = \arcsin(z/d)\]Since our survey volume is approximately 1 square degree, I only considered (sub)halos with \({\rm RA}<1\) and \({\rm Dec}<1\) degree. Further, I only took halos with \(d<60\times115\); this is because the lightcone is not complete for distances larger than this (this doesn’t actually make a difference, because there aren’t halos out that far). Finally, I recentered the survey by rotating the \((x,y,z)\) coordinates by angles \((\psi,\phi,\theta) = (-0.5,0,0.5)\).
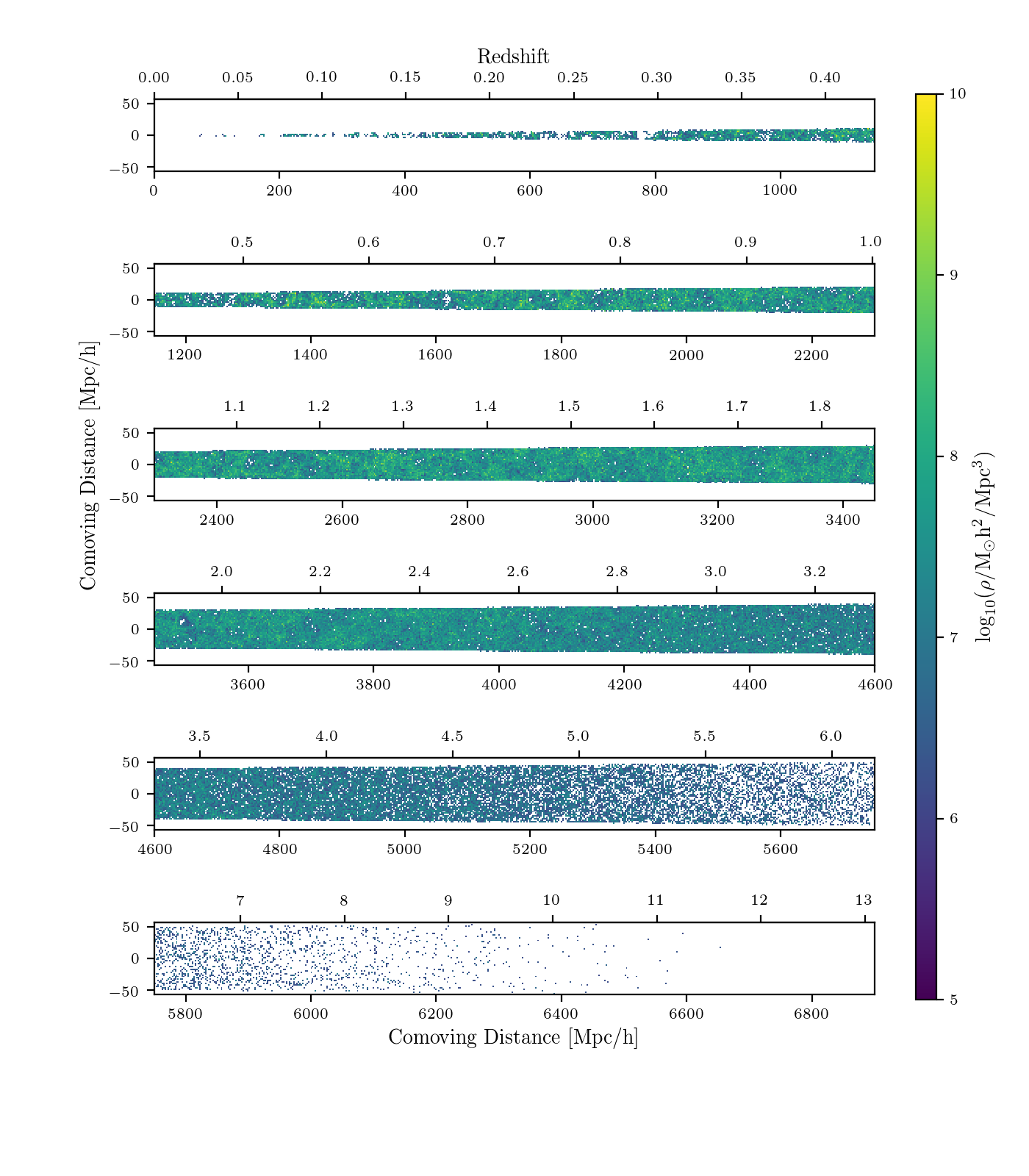
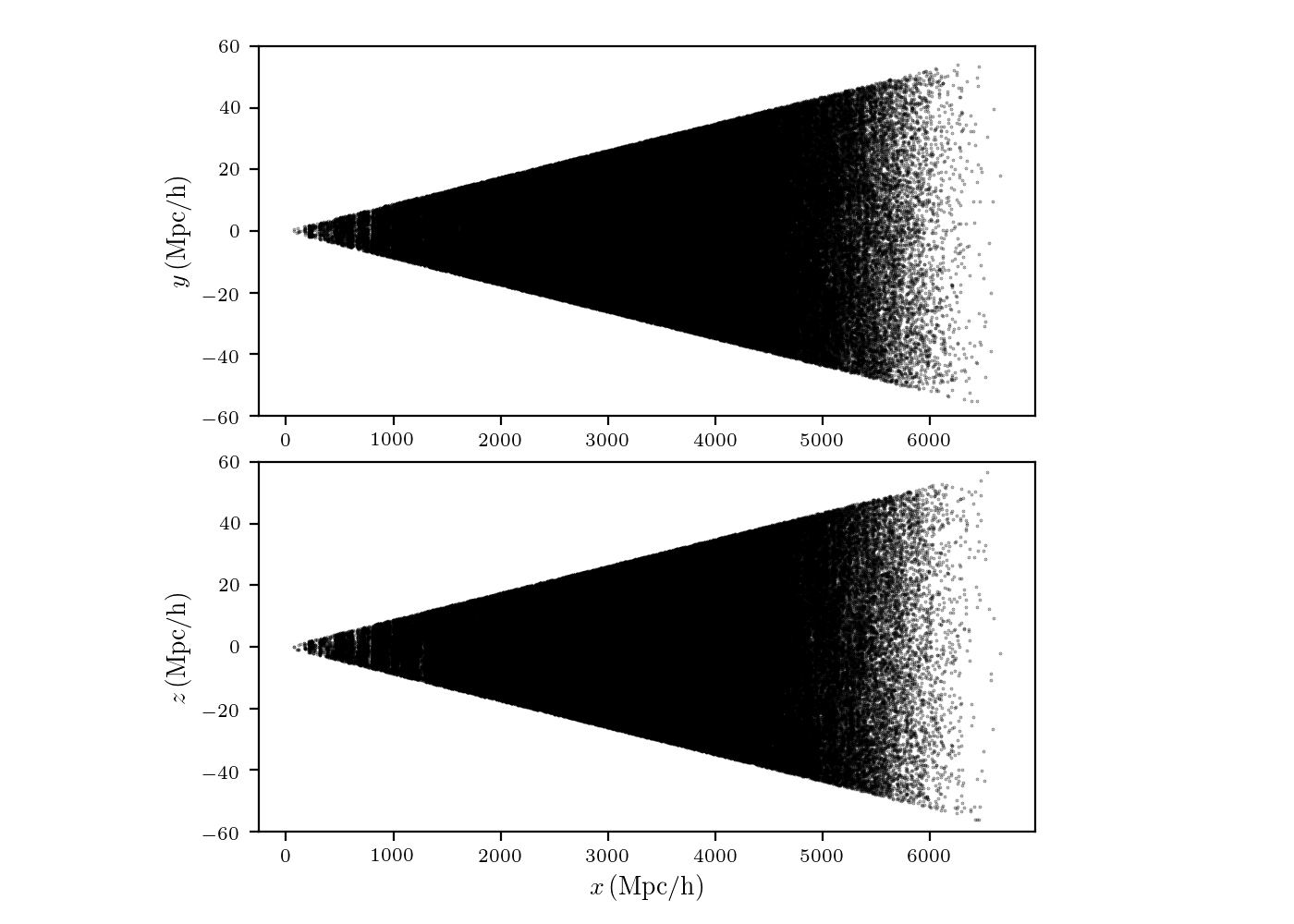
Here is a resulting scatter plot of the halo catalogue in the (new) cartesian coordinates (for the \(512^3\) simulation):
And a prettier plot, where I plot the mass density: