Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Mass Resolution
In a previous post, I determined that a box size of \(115\, h^{-1} {\rm Mpc}\) would allow us to construct the light cone for the ultra deep field down to redshift \(10\) without having to tile the simulations. With \(2048^3\) particles, this should resolve halos (with 100 particles) of masses above \(\sim 10^{9} h^{-1} M_*\).
Ideally, we would like to relate this halo mass to the galaxy luminosity to confirm that the resolution will be good enough for our purposes.
Magnitudes
The WFIRST will reach magnitudes \(m_{\rm AB} \sim 30\).
AB magnitude system
Based on spectral flux densities, \(f_{\nu}\):
\[m_{\rm AB} = -2.5 \log_{10} \left( \dfrac{f_{\nu}}{3631\, {\rm Jy}}\right)\]Recall \(1\, {\rm Jy} = 10^{-26}\, {\rm W} \,{\rm Hz}^{-1}\, {\rm m}^2\).
Absolute magnitude
The absolute magnitude is:
\[M = m - 5 \log_{10}({D_L/10 {\rm pc}})\]Where \(D_L\) is the luminosity distance, and is a function of redshift. I previously calculated the angular diameter distance, \(D_A\) , as a function of redshift here. The luminosity distance is then related to the angular diameter distance by \(D_L = (1+z)^2 D_A\).
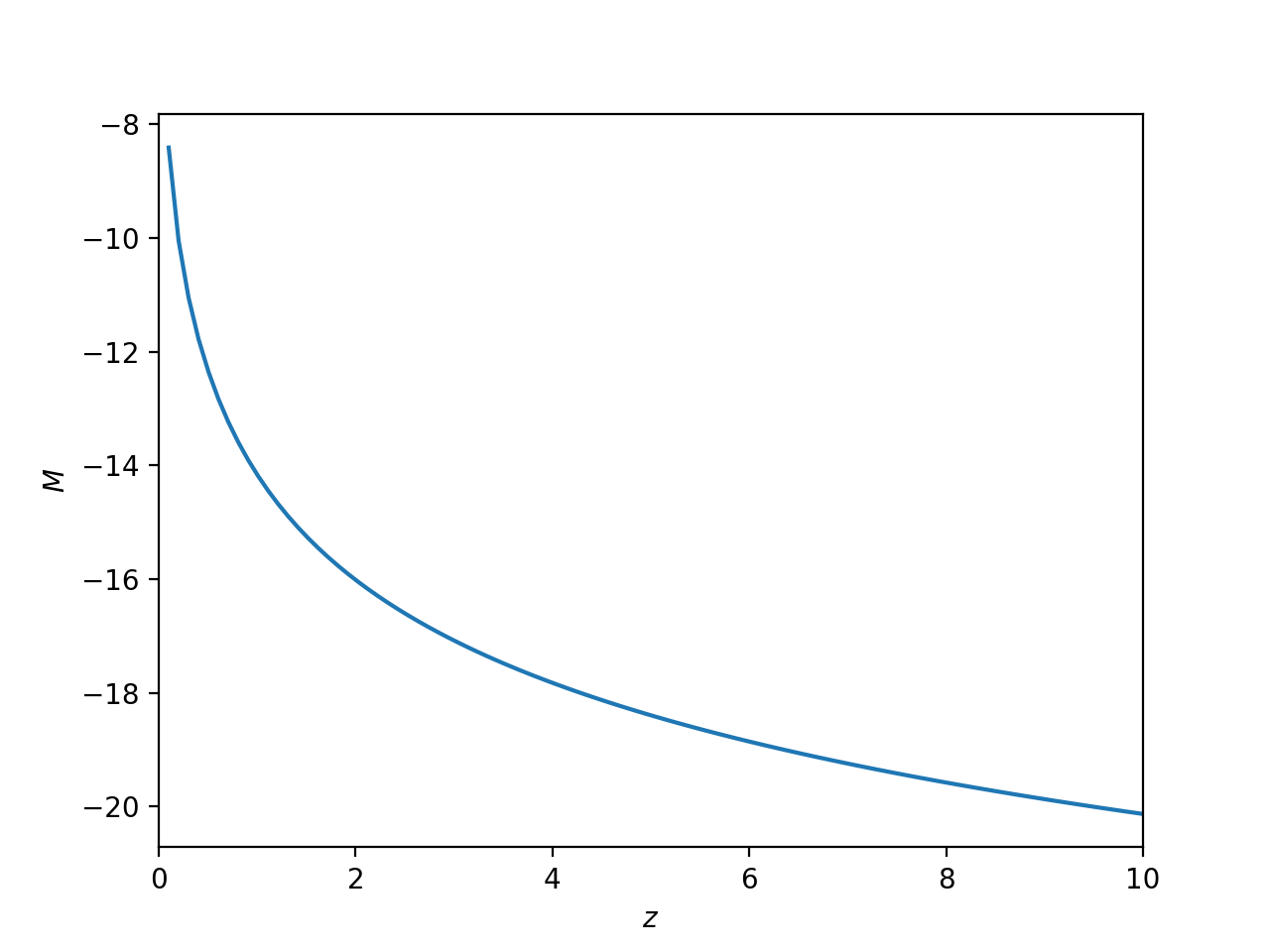
Here is \(M_{\rm AB}\) corresponding to \(m_{\rm AB} = 30\) as a function of redshift:
Stellar Mass to Luminosity
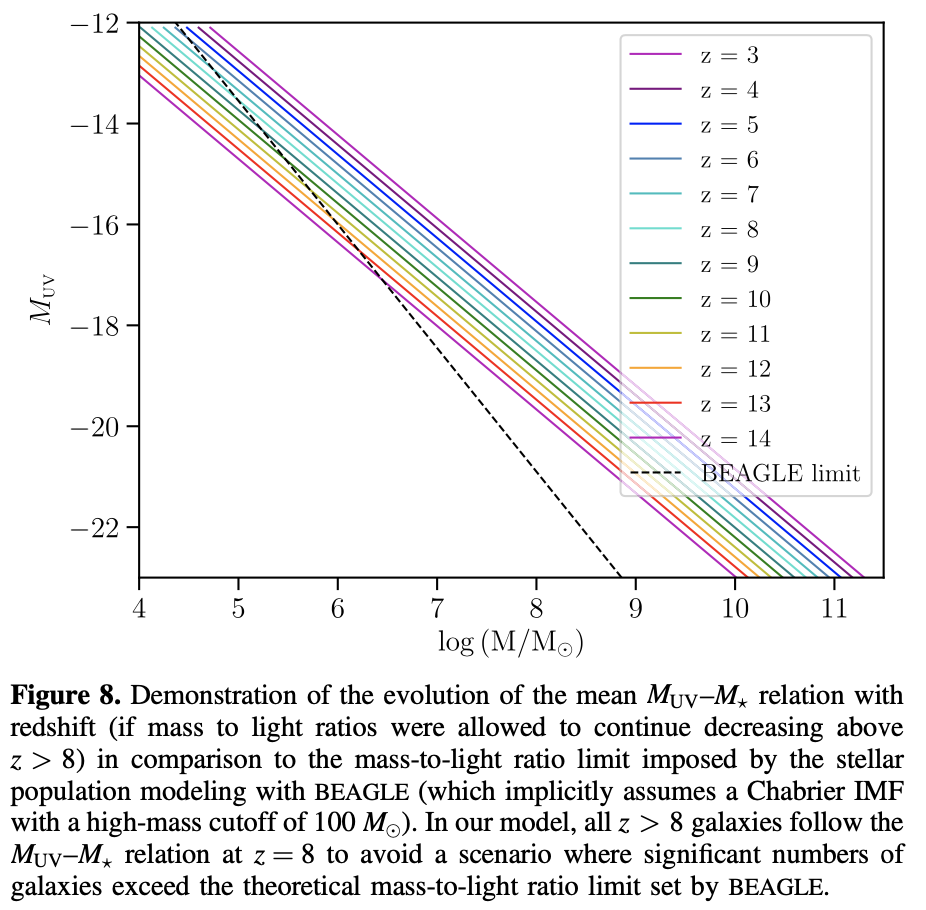
I plan to closely follow the methods from Williams et al. 2018 for obtaining stellar mass functions and UV luminosity functions down to redshift 10.
They conveniently provide this plot of the \(M_{UV}-M_*\) relation:
Questions
Does this UV magnitude correspond to the one I calculated above?
Clearly at redshift \(z=0\) you can view very dark objects… How do I get a minimum galaxy mass out of these plots?