Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Bubble Size Troubleshooting
I have code that calculates the ionized bubble around each galaxy as a Strogrem sphere. The solution seems reasonable down to about redshift 8, where the bubbles stop growing as rapidly as I expect. This results in an ionized volume that is too low (see my last post).
Overall, I expect a characteristic size of about 100 cMpc by redshift 6 (see here), but am instead getting a characteristic size of about 1 cMpc.
Sample Galaxies
I am considering the galaxies in between redshifts 6 and 6.5 in my “test” DREaM catalog (which only contains the most massive/brightest galaxies)
This is what the evolution of bubble sizes these sample galaxies look like:
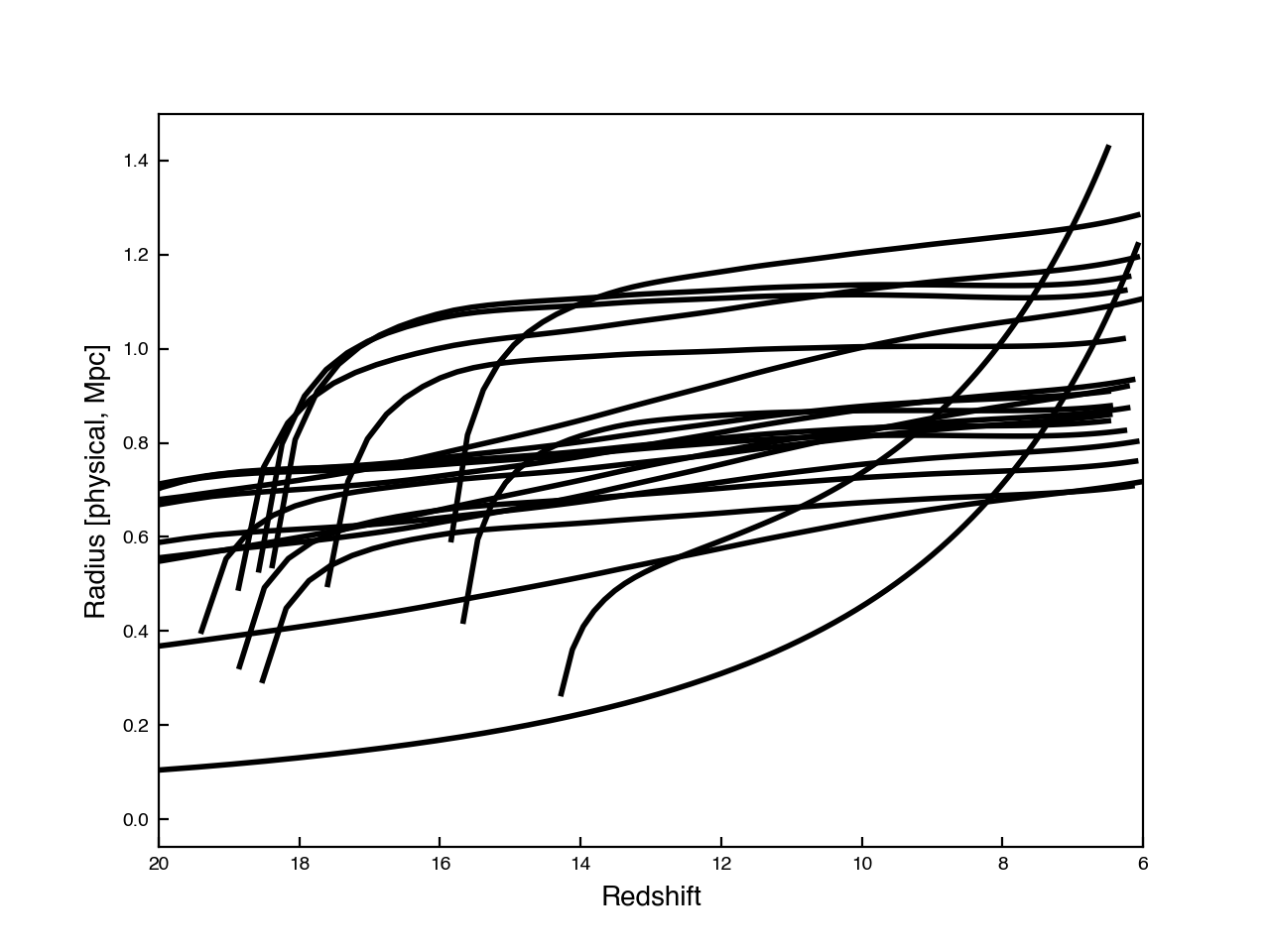
Add an ionized background
Where the solution seems to run into problems is around redshift 8, which is where ionized bubbles should be overlapping.
I attempted to approximate how much individual bubble sizes should increase by adding a background in the calculation; i.e. \(f_{ esc} \dot{N}_{ion}\) became \(f_{ esc} \dot{N}_{ ion} + \dot{N}_{background}\), where \(\dot{N}_{background} = \dot{n} Q V\), \(Q\) is the ionized fraction and \(V\) is the volume of the bubble.
This seemed to increases the final bubble sizes by a factor of 2, which isn’t quite enough.
Check numerical issues in integration scheme
I am using an implicit Euler scheme which should be stable. Nethertheless, I tried increasing the time steps, and switched to integrating along points that were linearly spaced in \(a\), the scale factor. These changes did not make any difference.
A “boost factor”
The Yajima et al. 2018 paper considers adding a boost factor. That is, they artificially increase the radius by a factor, f \(R \rightarrow f R\). They state that \(f=2\), e.g., corresponds to 8 similar galaxies in the overlapped regions.
Following a similar idea, I considered a boost, such that the volume increases by an extra factor of \(V\) every time it overlaps with a bubble (where N is the number of bubbles)
If we consider a mean free path \(l\) in which we will hit a bubble of size \(R\), and assume all bubbles are of similar size, we can argue
\(\dfrac{R^3}{l^3} = \dfrac{Q}{1-Q}\) and \(n= \dfrac{1}{l \sigma} = \dfrac{1}{3V}\left(\dfrac{Q}{ (1-Q)}\right)\).
Therefore, at every timestep, when a bubble increases by volume \(dV\), I multiple the volume by \(1 + \dfrac{dV}{3V_i)}\left(\dfrac{Q(z)}{ (1-Q(z))}\right)\). In reality, the growth of the bubbles should be stochastic, with discrete jumps every time bubbles overlap. However, since I am only concerned with the final bubble size, I’m not too worried about getting an averaged growth history.
Here is the resulting bubble sizes (physical Mpc):
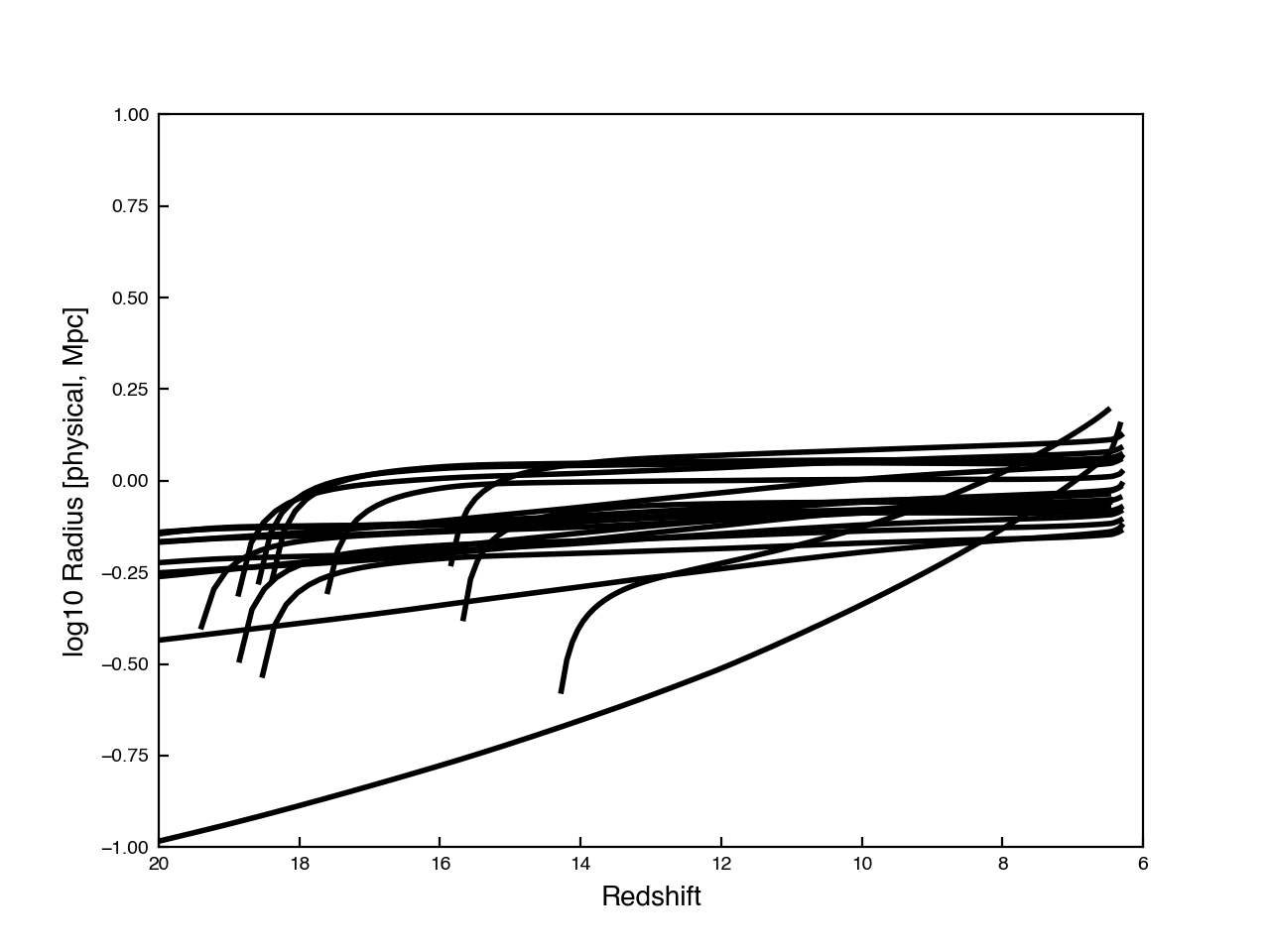
It’s a little hard to see what’s happening, since the bubble sizes tend to go to infinity. However, when I tested this same prescription with the galaxies between redshifts 7-8, I got a characteristic size of about 10 cMpc, which is around what I would expect. Therefore, I’m pretty happy with this method, and will run it on the full catalog and check the resulting ionization fraction.