Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Ionized Fraction
I outlined the reionization modelling in this post.
Here, I am going to begin to outline my calculation of the IGM ionized fraction in the DREaM catalog.
Calculation
The volume-filling fraction of ionized gas:
\[\frac{ dQ_{\rm HII} }{ dt} = \frac{ \dot{n}_{\rm ion} } {\langle n_H \rangle} - \frac{Q}{\bar{t}_{\rm rec}}\]Emissivity of Ionizing Photons
\(\dot{n}_{\rm ion}\) is the co-moving emissivity of ionizing photons. I outlined the calculation for this in previous posts (see here). This is what I am using for the “fiducial” reionization model. I will also explore other variations in the future.
Here is a plot, where I have added on measurements from the Lyman alpha forest:
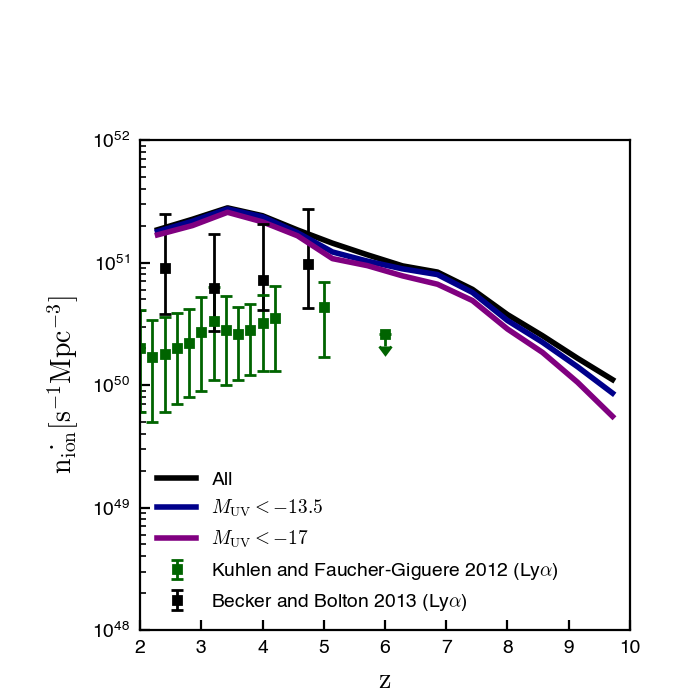
Our model agrees well with Naidu 2020 and Yung 2020, including the disagreement with the Ly\(\alpha\) forest constraints. I will try and plot other models on top of ours at some point (I’ll see if their data is tabulated, or if I have to read it off the plot somehow).
I need to read up a bit on the Ly\(\alpha\) forest constraints; how exactly they are obtained and why the Becker measurements disagree with the Kuhlen measurements. I think Yung 2020 shows you can reconcile things with a different \(f_{\rm esc}\) model.
Density of Hydrogen
The volume-averaged co-moving density of intergalactic hydrogen is given by:
\[\langle n_H \rangle = X \Omega_b \rho_c/m_{H}\]\(\Lambda\)CDM parameters:
- \(X=0.75\): the primordial mass-fraction of hydrogen (note this is what Yung+2020 uses. Naidu+2020 uses 0.75328, but I’m not quite sure where this is from.)
- \(\Omega_b=0.04893\): baryon density
- \(\rho_c = 3 H_0^2/8\pi G = 2.7754 \times 10^{11} h^2 M_\odot {\rm Mpc}^{-3}\): critical density
- \(m_H\): mass of a hydrogen atom
I calculated \(\langle n_H \rangle =1.9\times 10^{-7} cm^{-3}\), which is identical to what is found in Madau & Dickinson 2014.
Hydrogen Recombination Time
The recombination time of ionized hydrogen in the IGM is given by:
\[t_{\rm rec} = [ C_{\rm HII} \alpha_B (1 + (1-X)/4X) \langle n_H \rangle (1+z)^3 ]^{-1}\]The clumping factor, \(C_{\rm HII} = \langle n_H^2 \rangle/ \langle n_H \rangle^2\) is the redshift-dependent HII clumping factor that models the inhomgeneity of the IGM.
- Naidu2020 sets this to 3
- Finkelstein2019 and Yung2020 use numerical predictions from the radiation-hydrodynamical simulation by Pawlik et al. (2015). In this, \(C_{\rm HII}\) evolves from 1.5 to 4.8 between z=14 and 6.
I will start by using just a constant value (e.g. 3) to get this working, but I want to implement the Pawlik model, and see how much this changes things.
\(\alpha_B\) is the the temperature-dependent case B recombination coefficient for hydrogen. There are some variations here to what people use. There is a good description of what “case B recombiation” means in Raicvic et al. 2014.
- Naidu2020 states \(\alpha_B = 2.6 \times 10^{-13} (T/10^4 {\rm K})^{0.76} {\rm cm^3 s^{-1}}\) uses \(T=10^4\) (They cite Shull et al. 2012; Robertson et al. 2013, 2015; Pawlik et al. 2015; Sun & Furlanetto 2016). It looks like they are taking this directly from Sun & Furlanetto 2016.
- Finkelstein2019 and Yung2020 cite Hui & Gnedin (1997) and use \(T=2 \times 10^4\) (Finkelstein cites Robertson 2015).
- Shull+2012 say \(\alpha_B = 2.59 \times 10^{-13} (T/10^4 {\rm K})^{-0.845} {\rm cm^3 s^{-1}}\) and cite (Osterbrock & Ferland 2006). I’m wondering if the exponent is a typo, becuase it doesn’t seem quite right. They state “for typical IGM ionization histories and photoelectric heating rates, numerical simulations predict that diffuse photoionized filaments of hydrogen have temperatures ranging from 5000 K to 20,000 K (Davé et al. 2001; Smith et al. 2011)”
Given all this, I will follow Sun2016, Naidu2020 and use \(10^4\) K as the fiducial temperature, but explore the effects of this assumption.