Reionization Shell Model Part III

I am planning to calculate the reionized region around each galaxy in the DREaM catalog using a simple shell model.

This is a continuation from previous posts, Part I and Part II.

Summary of previous post

As outlined in the previous post, I calculated the volume around each galaxy to be:

\(V(t) = f_{\rm esc}\dfrac{e^{- n_H C \alpha t}}{n} \int e^{ n C \alpha t} \dot{N}_{\rm ion} dt\),

which gave values that I suspect are too large, as shown here:

Expected bubble size

Some relevant papers (this was from a quick search, not an in-depth literature review):

Wyithe & Loeb 2004

Furlanetto & Oh 2005

Yajima et al 2018

Tilvi et al. 2020

The most relevant plot was in Yajima et al., which shoes the expected (physical) size of bubbles for individual galaxies:

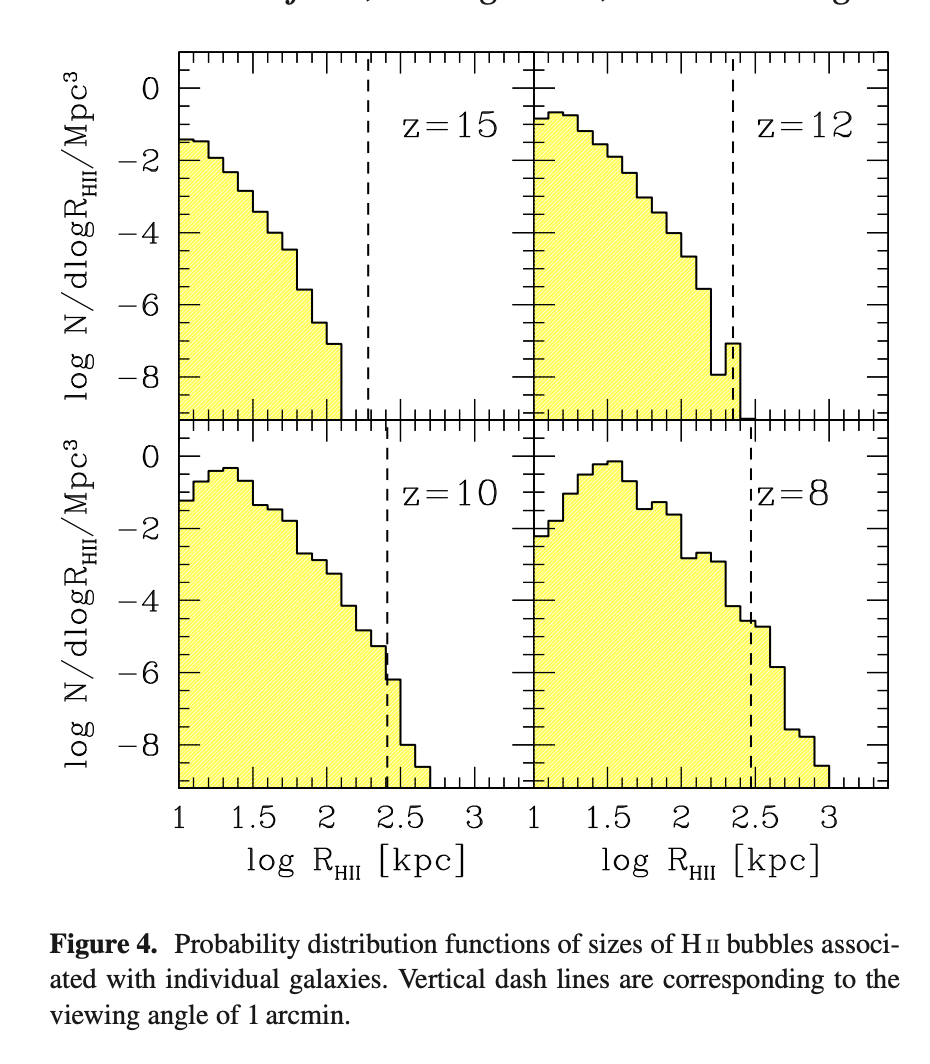
Looking at these papers, It seems like ~1Mpc (physical), or ~10Mpc (comoving) is about the maximum size of bubble you should expect around an individual galaxy.

Therefore, my calculation is likely not realistic. I think that this might be because I used \(n_H\) at the present day, when really it should be a function of redshift.

Derivation

I had begun with this equation (from Magg et al. 2018..):

\[\dot{V} = \dfrac{f_{\rm esc}\dot{N}_{\rm ion} (t)}{n_H} - n_H C \alpha V\]

this equation says that the volume of ionized regions grows with ionizing radiation, and decreases with recombinations. Clearly, the mean hydrogen density, \(n_H\), should be dependent on time.

Further, looking at Yajima et al., I think I should include the cosmic expansion (which was neglected in Magg+, since it cosmic timescales were large compared to the timescales they considered.)

Therefore, our equation becomes (where I have used primes to denote \(d/dz\))

\(\dot{V}(t) = \dfrac{f_{\rm esc}\dot{N}_{\rm ion} (t)}{n_H(z)} + (3H(z) - n_H(z) C \alpha) V(t)\) \(- H(z) (1+z) V'(z) = \dfrac{f_{\rm esc}\dot{N}_{\rm ion} (z)}{n_H(z)} + [3H(z) - C \alpha n_H(z) ] V(z)\) \(- H(z) (1+z) V'(z) = \dfrac{f_{\rm esc}\dot{N}_{\rm ion} (z)}{n_H^0 (1+z)^3} + [3H(z) - C \alpha n_H^0 (1+z)^3] V(z)\)

I cant solve this as pretty as I did before, but I can use on ODE solver (either in python or write my own). This equation will also require calculating \(\dot{N}_{\rm ion}\) and \(H(z)\) at each time step in the ODE calculation. This may be significantly slower, so we might want to come up with approximations if the speed becomes prohibitive.

Next steps

1. Write code to do this for the one galaxy, check the answer makes sense and the speed is okay
2. Once I think this makes sense, write code to do this for all galaxies
3. Plot the reionized regions, see if they agree with radiative transfer simulation findings. (i.e., is the percentage of ionized regions reasonable?)

---

« Reionization Shell Model Part II

A Closer Look at SFHs in DREaM »