Double Alpha Profile Stability

As I said in the last post, I will set up a “Double Alpha” profile. Here I am checking the stability of the IC code.

Parameters

I changed the alpha parameters slightly from the last post.

• \(\alpha_{dm}\) = 0
• \(\alpha_{stars}\) = 1
• \(r_{s,dm}/r_{s,stars}\) = 10
• \(M_{dm}/M_{stars}\) = 200

I will run this with N=1e5 for initial testing. The simulations we use will have 1e7 particles.

Check 1: Initial Positions

Here are the initial positions

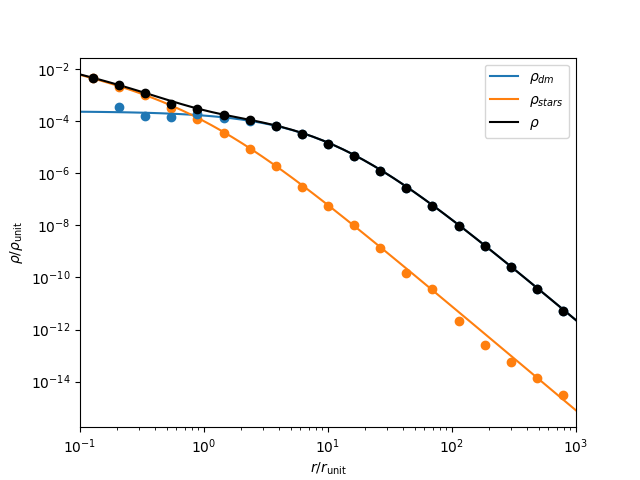
Looks like this part is working. If the velocities are assigned correctly, this should be stable when evolved in isolation.

Check 2: Initial Velocities

If the energy of the particles make sense, the particles should all initially be bound—i.e., they should all have a positive “binding” energy, \(\mathcal{E} = -\phi(r) - \dfrac{1}{2} v^2 > 0\). Additionally, the maximum energy should be \(-\phi_0 = \dfrac{4 \pi G \rho_{s,dm}}{(3-\alpha_{dm})(2 - \alpha_{dm})} + \dfrac{4 \pi G \rho_{s,stars}}{(3-\alpha_{stars})(2 - \alpha_{stars})}\)

Here is the distribution of energies, with \(-\phi_0\) plotted as a vertical line.

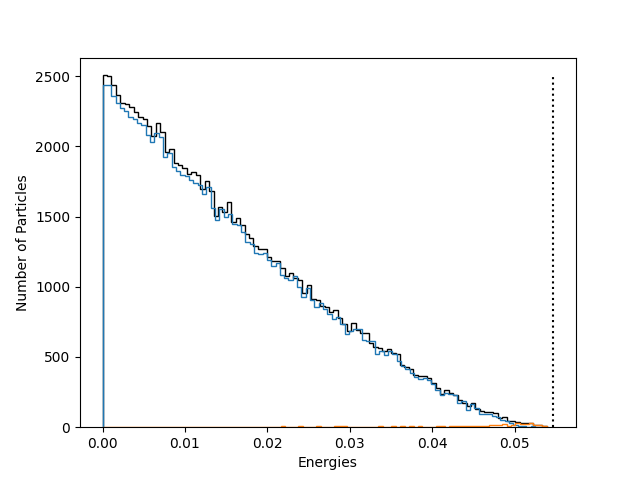
The distribution of energies fall in the correct range, which is reassuring that the range of velocities are correct.

Run in Isolation

Then I ran it in isolation, which is the real test for stability. The vertical line is the relaxation radius:

This looks good!

Next Steps

1. Decide a fiducial orbit, calculate the snapshot spacing (so that there are 10 snapshots per orbit)
2. Run the fiducial case for Bradley
3. Decide a grid of simulations
4. Run simulations: See if Peter wants to get involved again, or if Bradley wants to run them. Otherwise I’ll do this part.
5. Do this all for a higher resolution (\(10^7\) particles)

---

« Two Component ICs

Fiducial Orbit »