Impulse Approximation

For the tidal stripping paper III revisions, the reviewer pointed out that the physical interpretation of our energy-based model is unclear. In particular, they argue that the impulse approximation suggests that the change in a particle’s energy should be larger at large radii. Therefore it is not clear why you would expect tidal stripping to be an energy-dependant process, and further why our model, which basically changes particle energies by a constant amount would work.

Andrew suggested that this is because we really only need to get the change in energy close to the boundary right. Particles that get stripped we don’t really care about their energies. Interior particles that will not get stripped, we again do not need to get right.

Another important thing to keep in mind is that our model suggests there is a constant change in the self-bound energy. As the system loses mass, the particles will become less bound from the decrease in masss, even if they do not receive a change in velocity.

We are going to add a section to the paper addressing the energy-truncation model in this framework.

The impulse approximation

The impulse approximations states that the change in energy should be:

\[\Delta E = \dfrac{1}{2} (\mathbf{v} + \Delta \mathbf{v})^2 -\dfrac{1}{2} \mathbf{v}^2= \mathbf{v} \cdot \Delta \mathbf{v}+ \dfrac{1}{2} (\Delta \mathbf{v})^2\]

and the change of velocity should scale with radius:

\[\Delta \mathbf{v} = \dfrac{2 G M_p}{v_p b^2} [-x,y,0]\]

Particle removal in phase-space

If we look at the particles in radius–velocity phase space, we can see how the radii, velocities and energies change. This allows us to see how properties change as a function of radius, velocity and energy (which are contours in phase space).

1. Change in velocity

The change in velocity scales with radius as expected:

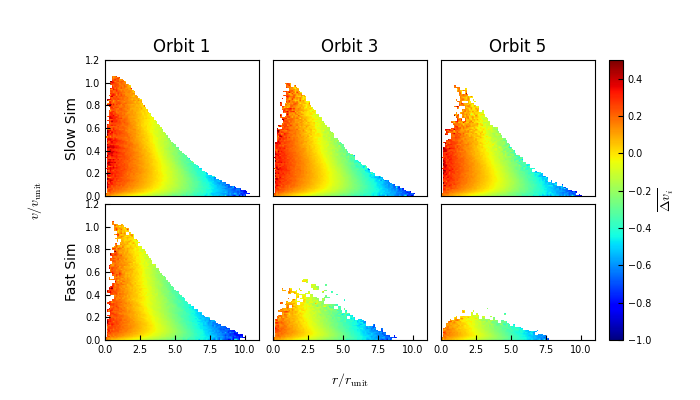
2. Change in radius

The change in the radii of particles are mostly zero, except on the edges of the phase-space distribution (i.e. at a constant energy). Overall, it seems that the change in particle radius is primarily a function of energy.

3. Change in energy

The resulting change in self-bound energy is also primarily a function of energy. The change of energy in the centre is mainly due to the change in mass of the self-bound remnant. This supports the idea that energy really only changes on the outskirt of the system, and the inner particles are shielded.

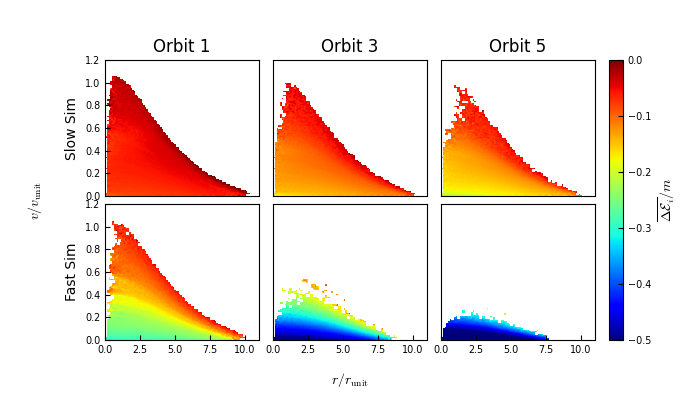
Delta E

If we consider the change of energy of each particle that is still self-bound after orbit X (compared to the initial energy), we find that the average change of energy decreases with increased radius and decreased binding energy. Particles that are the most bound and/or have the smallest radius have the largest drop in “bindedness”:

This is because the overall system decreases in mass. If you look at the earlier plots, what is really happening is that for highly bound particles/ particles at small radii, the energy of individual particles is ONLY changing because the overall potential of the system is changing. The particles on the outskirts are getting a larger change in their individual velocities/radii, but the resulting change in their “binding” energy is small.

Looking specifically at Orbit 3, we show the two components from the \(\Delta E\) impulse approximation (red and blue), and also the change in binding energy that was shown in the previous plot (black):

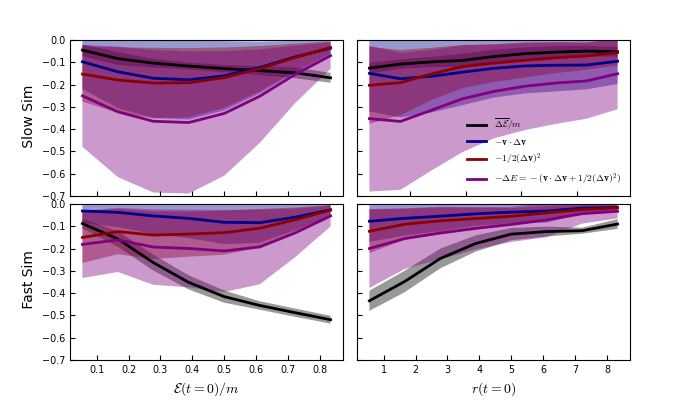
The change in energy (\(-\Delta E\), purple) is mostly constant, except at the center/for the most bound particles (which are likely shielded from the tidal field). The purple and black do not agree because of the different definition of energy (i.e. the change in the mass used to calculate the self-bound potential). The individual components (red and blue) do not behave in a very different way.

Both components of the \(-\Delta E\) equation (blue and red lines) scale slightly with radius, as expected, but the difference is slight. Note it is a slightly different value than what was plotted in the phase plots (\(\Delta {\rm mag} (\mathbf{v})\); this is the difference in the magnitude, not the magnitude of the difference vector).

What to include in write-up

Overall, I want to demonstrate that (A) the constant boost in energy is mainly due to the change in mass of the self-bound system and (B) although the change in velocity scales with radius, the change in energy along the boundary is constant.

Therefore, the picture is that the tidal fields pull off the least bound particles first (we will include a section on the deforming-bowl picture to describe this), and all the particles have a shift in energy due to the lower mass of the self-bound system.

I think I will only include the phase-space plot of the change in energy in the main text, as I think this encompasses the whole picture. I might include a few more plots in an appendix if that will make our point clearer, or we can leave a deeper discussion of this point for a future work.

For example, a future project (not necessarily for me!) could be based on understanding the physical interpretation of energy-based models. It could look into some/all of the following:

1. The change of energy of individual particles, and what is contributing to it
2. A non-sharp truncation in the distribution function that captures the Fast Sim better (what is the physical component that dictates this?)
3. Some of the existing work that has been done by James + students on the details of mass loss
4. A better prediction of eta… maybe either having a time dependant eta, or doing the boosted potential calculation with the centrifugal term
5. Really understanding what the shift + truncation in the distribution function is doing (see some of the discussion in Paper I)

---

« Two Component System

General Model for Two-Component Satellite »