Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Disk ICs with Halo Potential
In my last post I outlined how to set up ICs for a isolated disk, following Hernquist 1993.
In this post, I’ll add in a fixed potential for the halo.
The Halo Model
The halo will be NFW:
\(\rho(r) = \dfrac{\rho_0 r_s^3}{r(1+r_s)^2}\),
and the gravitational potential is given by:
\[\Phi(r) = - \dfrac{4 \pi \rho_0 r_s^3}{r} \ln \left( 1 + \dfrac{r}{r_s}\right)\]Including the Halo Potential in the ICs
The potential of the halo can be added to the potential of the disk when calculating the particle velocities.
This alters the calculations of \(\kappa\) and \(\Omega\), and therefore the radial and azimuthal velocities.
Simulating
I checked this by evolving the ICs in a modified form of Gadget, which includes a fixed NFW background potential.
The NFW halo was given the parameters: \(M_{\rm vir} = 5.8\), \(r_{vir}=10\) and \(r_s=1\).
Here is how it evolved:

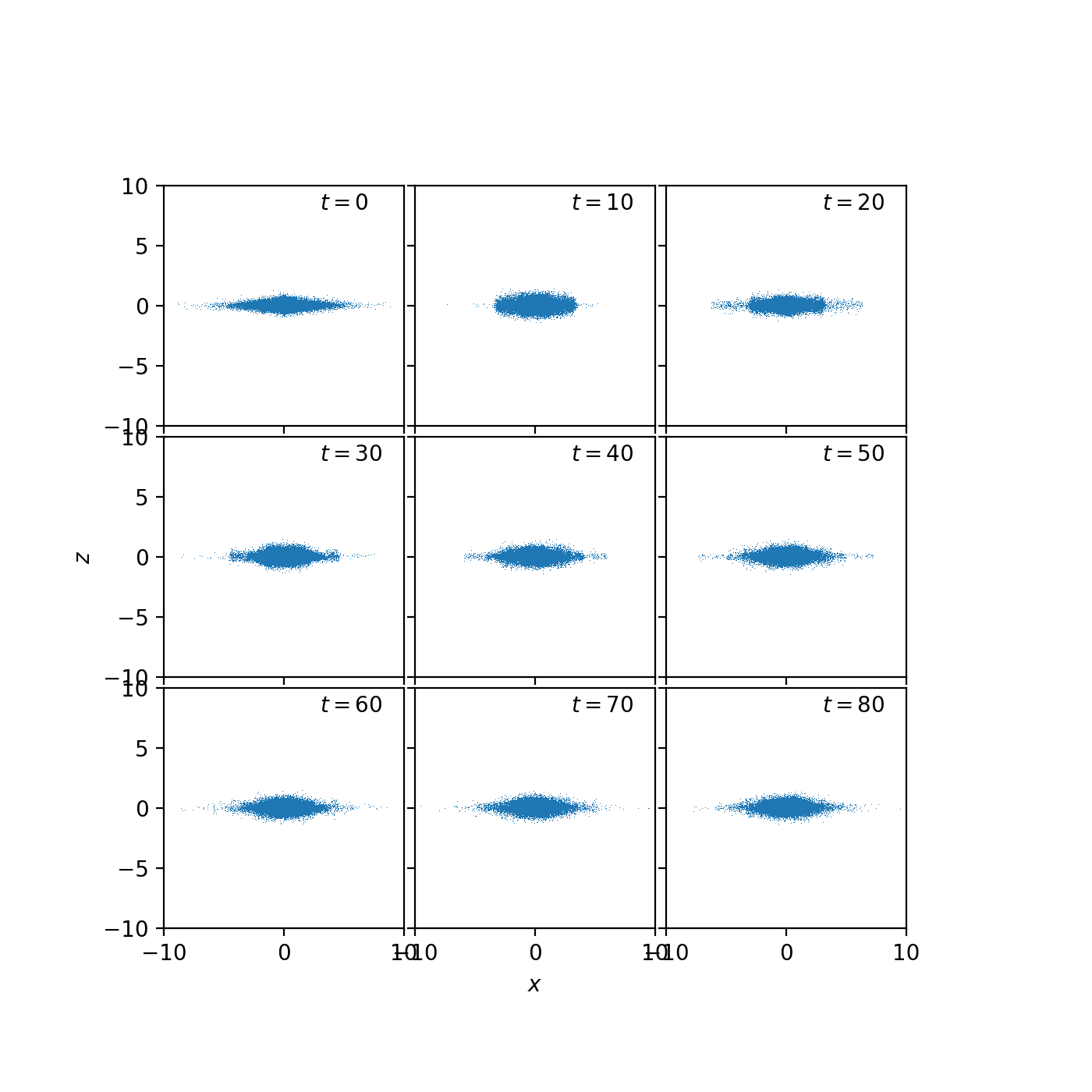
It’s not perfectly stable, but OK… it might be that my gravitational softening length is too big, or I have an error somewhere. It could also be that I didn’t add in the softening of the radial dispersion, as suggested in Hernquist 1993.