Reionization Shell Model Part IV

I am planning to calculate the reionized region around each galaxy in the DREaM catalog using a simple shell model.

This is a continuation from previous posts, Part I and Part II, and Part III.

ODE Scheme

The ODE I want to solve is:

\(- H(z) (1+z) V'(z) = \dfrac{f_{\rm esc}\dot{N}_{\rm ion} (z)}{n_H^0 (1+z)^3} + [3H(z) - C \alpha n_H^0 (1+z)^3] V(z)\),

where \(V\) is the physical volume of the bubble

Or, equivalently,

\[A(z) = - \dfrac{f_{\rm esc}\dot{N}_{\rm ion} (z)}{n_H^0 H(z)(1+z)^4}\] \[B(z) = \dfrac{C \alpha n_H^0 (1+z)^2}{H(z)} - \dfrac{3}{1+z}\] \[V'(z) = A(z) + B(z) V(z)\]

I will solve this using an implicit Euler method (as in Magg+2018)

\[A_i = - \dfrac{f_{\rm esc}\dot{N}_{\rm ion,i} }{n_H^0 H(z_i)(1+z_i)^4}\] \[B_i = \dfrac{C \alpha n_H^0 (1+z_i)^2}{H(z_i)} - \dfrac{3}{1+z_i}\] \[V_{i+1} = V_i + \Delta z V'_{i+1}\]

Which can be rearranged to:

\[V_{i+1} = [V_i + A_{i+1}\Delta z] (1-B_{i+1}\Delta z)^{-1}\]

This can be integrated from \(z_0 = z (t_{\rm start})\), with an initial condition of \(V_0 = 0\). for now I’ll loop through to solve for the volume, since I need to loop through these time points anyway to get \(\dot{N}_{\rm ion}\) from fsps. I will need to do some timing tests, and see if I need to speed this up for the full catalog.

Results

Here are the results for my test galaxies:

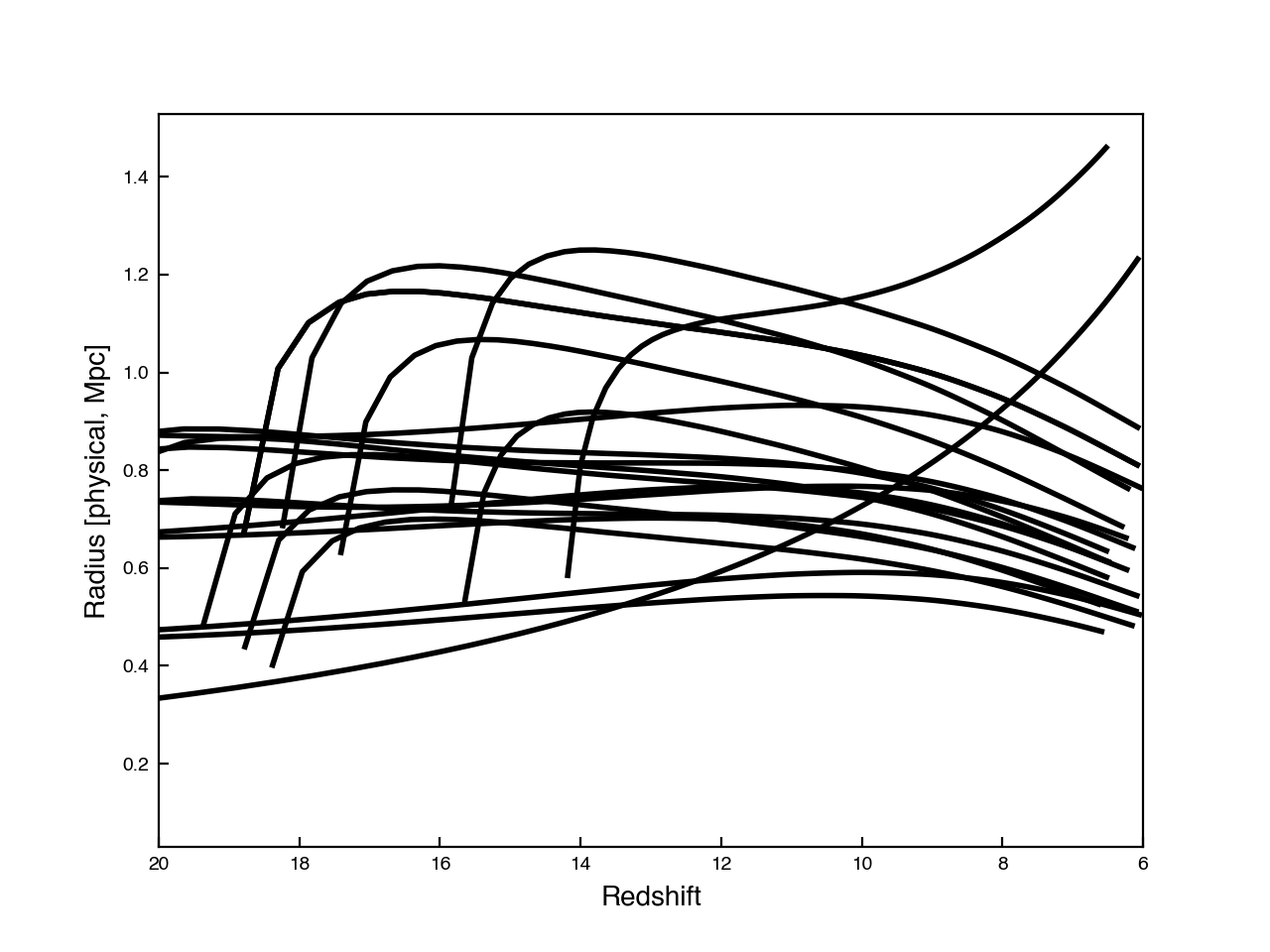
This actually looks quite reasonable!

Next Steps

1. Write code to do this for all the galaxies, make sure it is fast enough.
2. Plot the ionized regions, see if this agrees with what is expected

---

« A Closer Look at SFHs in DREaM

Reionization Shell Model Part V »