Nicole Drakos
Research Blog
Welcome to my Research Blog.
This is mostly meant to document what I am working on for myself, and to communicate with my colleagues. It is likely filled with errors!
This project is maintained by ndrakos
Topology of Reionization Part III
I outlined my method for calculating the distribution of bubbles in my previous post. I noted that the ionized regions might be too small. In this post, I’m looking into this in more detail.
Comparison of Ionized Fraction
If I compare the IGM neutral fraction calculated directly from the galaxies (dotted line) with the area of the survey that has an ionized bubble (solid line), I find:
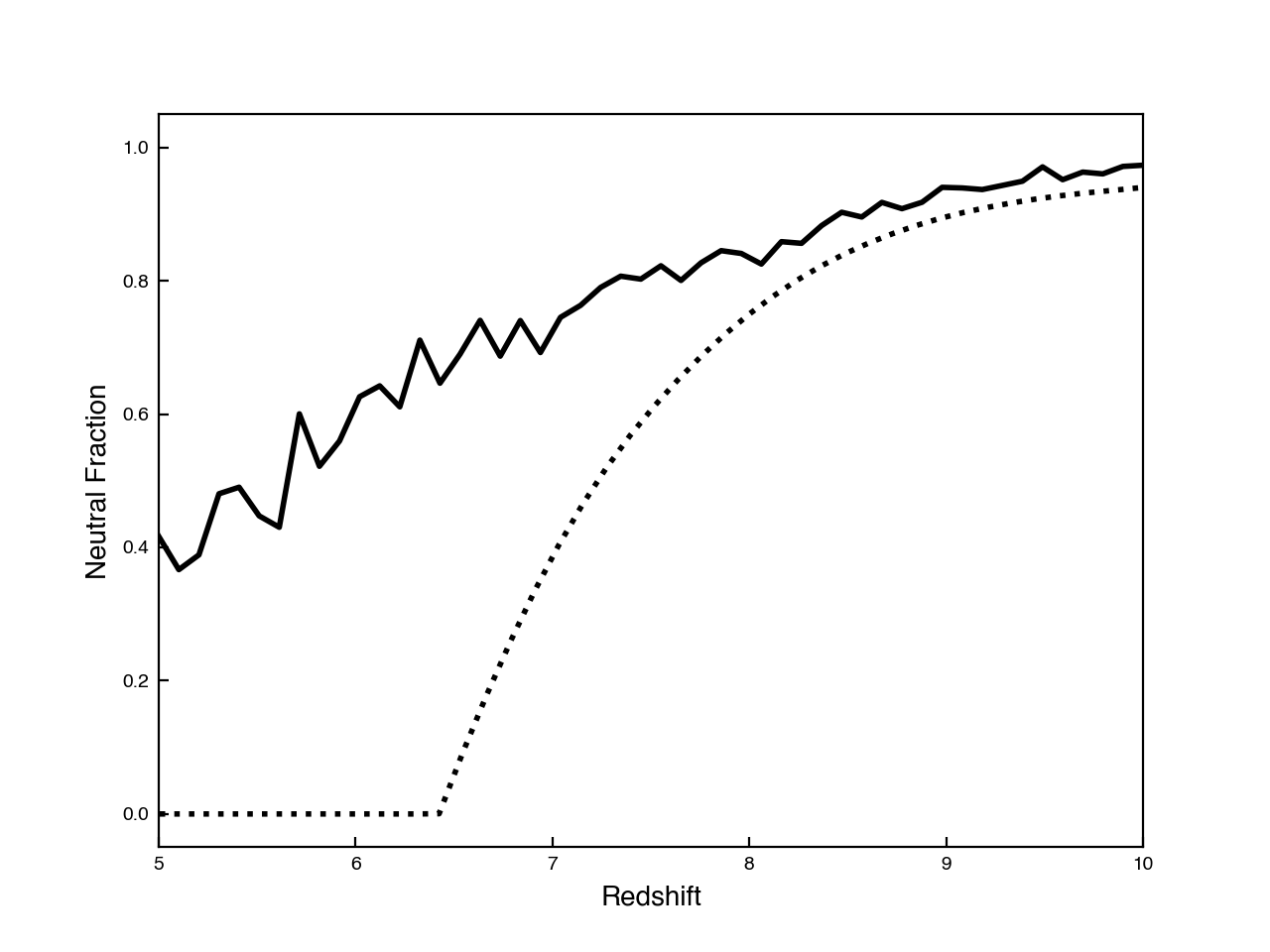
Clearly there is a descrepancy between these two calculations!
Compare Calculations
1. Directly from galaxies
The direct calculation was outlines in this post.
To summarize, I used:
\(-(1+z)H(z) \dfrac{ dQ_{\rm HII} }{ dz} = \dfrac{ \dot{n}_{\rm ion} } {n_H^0} - \dfrac{Q}{\bar{t}_{\rm rec}}\) (Eq 1)
where
- \(\dot{n}_{\rm ion}\) is calculated from adding up the ionizing photon contribution from all galaxies
- \(n_H^0\) is the comoving number density of hydrogen and is approximately equal to \(1.9\times 10^{-7} cm^{-3}\).
- \(t_{\rm rec}\) is the recombination time, and is given by \(t_{\rm rec} = [ C_{\rm HII} \alpha_B (1 + (1-X)/4X) n_H^0 (1+z)^3 ]^{-1}\).
- \(X=0.75\) is the hydrogen fraction
- \(C_{\rm HII} = 3\) is the clumping factor
- \(\alpha_B = 2.6 \times 10^{-13} (T/10^4 {\rm K})^{0.76} {\rm cm^3 s^{-1}}\), with \(T=10^4\) K. This is approximately \(2.6 \times 10^{-13}\)
The first term on the RHS is the source term. It is the number of ionized photons produced by galaxies, divided by the present-day hydrogen number density. The second term on the RHS accounts for the recombination of hydrogen atoms.
2. From bubbles
The evolution of the volume (this is the physical not the comoving volume), was outlined in this post and this post:
\(- (1+z) H(z) \dfrac{V}{dz} = \dfrac{f_{\rm esc}\dot{N}_{\rm ion} (z)}{n_H (z)} + 3H(z)V - C \alpha n_H (z) V(z)\) (Eq. 2)
In this equation, \(n_H\) is the mean hydrogen density within the ionized bubble. I have been using \(n_H^0 (1+z)^3\). This does assume no environmental differences between galaxies.
The first term on the RHS is the source of photons. The second term on the RHS reflects the expansion of the universe. The third term represents the recombination of hydrogen atoms.
Comparison
These two equations are very similar with a couple of noticeable differences
-
The source term is divided by the present-day number density in Eq.1, but is time-dependent in Eq 2. This is because Eq 1 is in co-moving coordinates, and Eq 2 is in physical coordinates. If you convert Eq. 2 to the comoving volume, the factors of \((1+z)\) agree.
-
Eq 1 does not include a term for the expansion of the universe. This is fine, since we can assume that the volume of ionized and un-ionized regions expand at the same rate.
-
The recombination rate does not have the \((1 + (1-X)/4X)\) term in Eq 2. This term is \(1.08\), so it should make very little difference, but I will include it in Eq 2 from now on.
So far this all looks fine!!
Double check code
Double checking my code, I found I forgot the Hubble expansion term. This makes very little difference though.
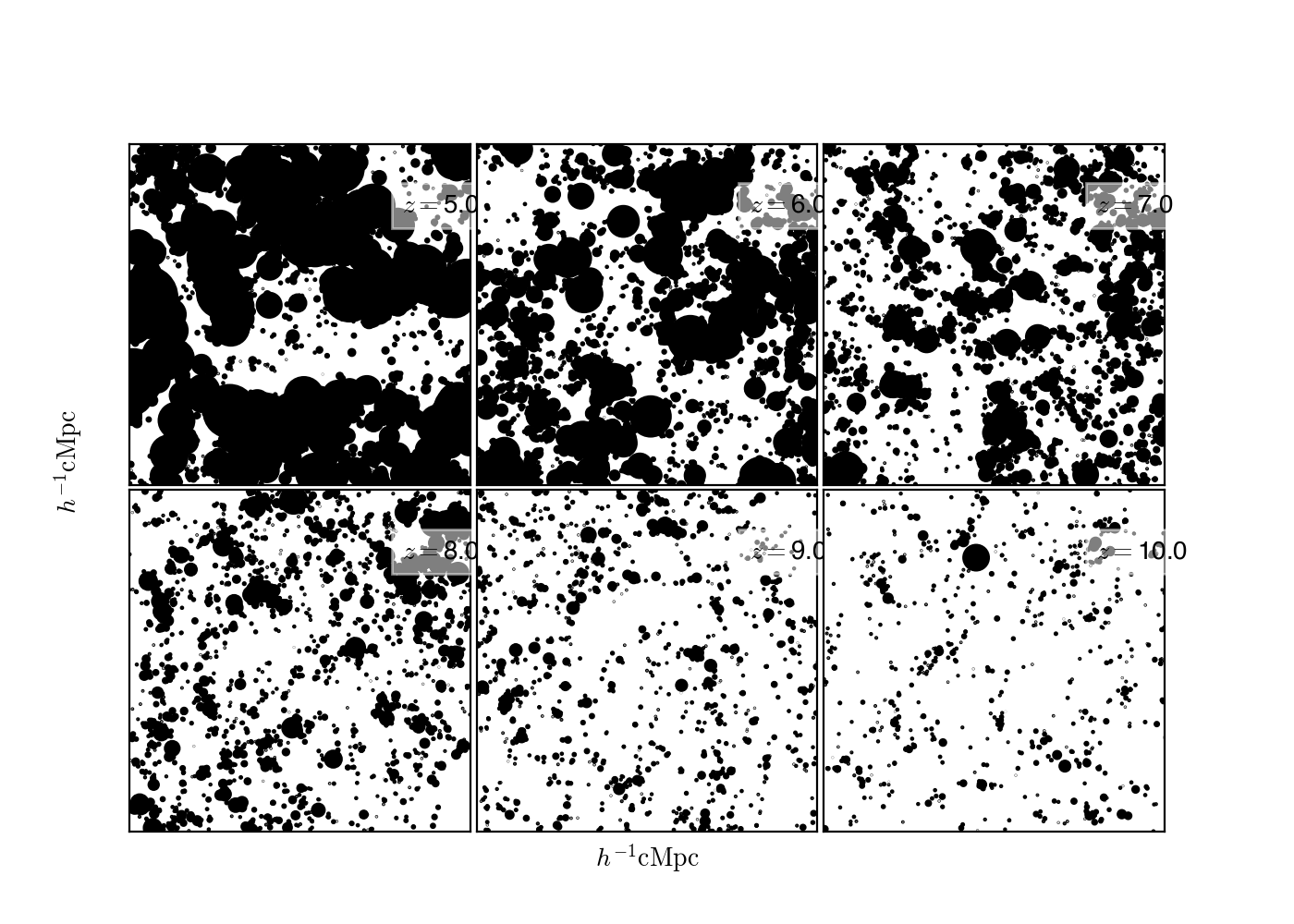
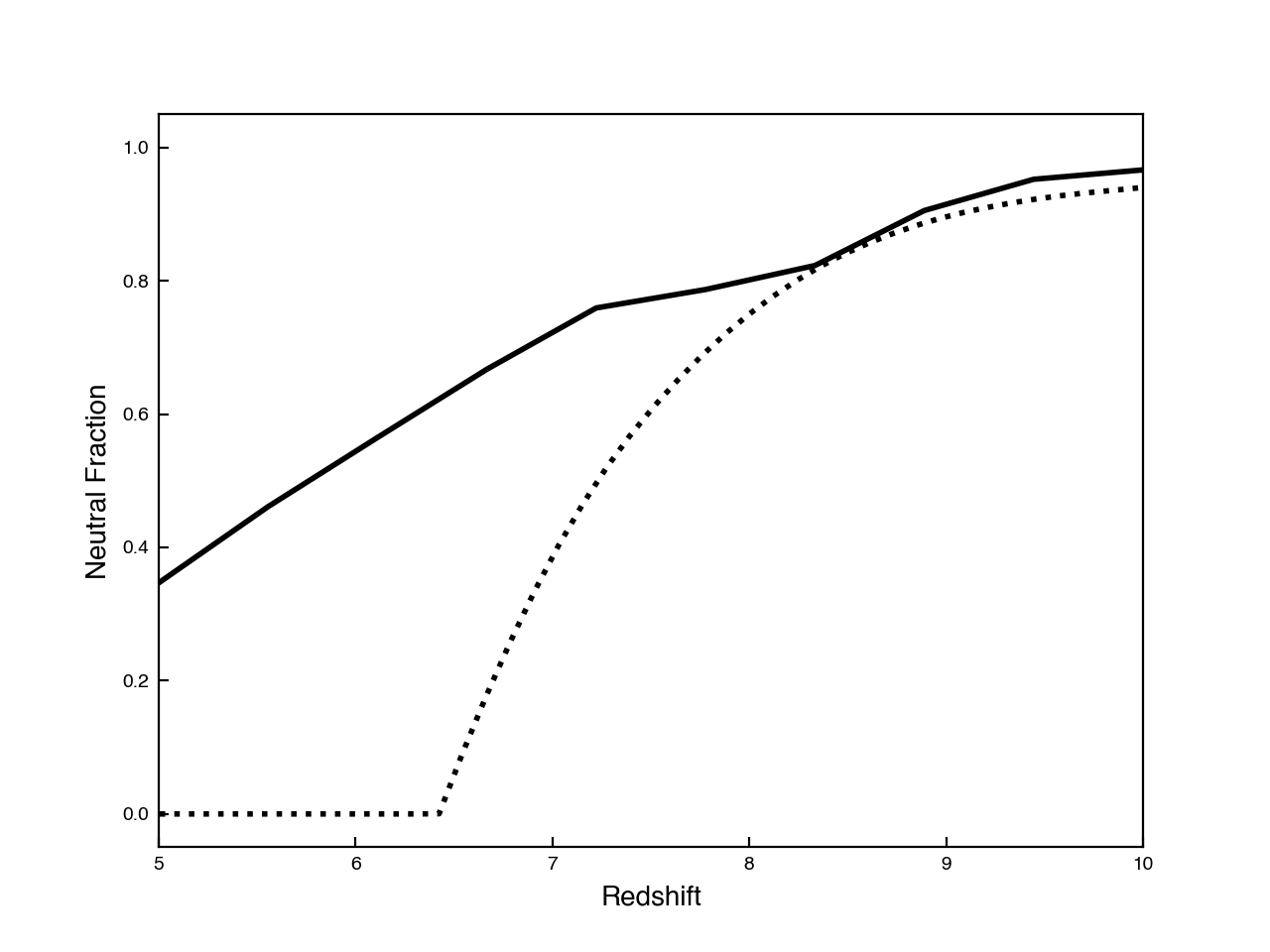
(note that I used less points in the last plot, which is why it looks smoother than the previous version.)
What’s next?
I still need to do a careful comparison of my bubble distributions, to see if the sizes look right. This will help guide me to solve the problem! It might be due to one of the simplifications/modelling assumptions.